ස්කන්ධ සංස්ථිති නියමය
| මෙම ලිපිය |
| සන්තති යාන්ත්ර විද්යාව |
|---|
| පිළිබඳ ලිපි මාලාවේ කොටසකි |
 |
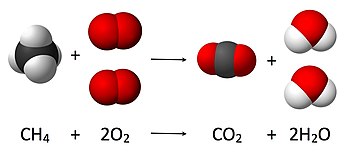
ස්කන්ධ සංස්ථිති නියමය එසේත් නැත්නම් පදාර්ථ සංස්ථිති නියමය (හෝ ලොමොනොව් ලැවෝෂියර් නීතිය) කියා සිටින්නේ සංවෘත පද්ධතියක ස්කන්ධය පද්ධතිය තුළ කුමක් සිදුවුවත් නියතයක්ව පවතින බවයි. එනම් පදාර්ථය නැවත සකස් කළ හැකි වුවත් මැවීමට හෝ විනාශ කිරීමට නොහැකි බවයි. එමගින් කියවෙන්නේ සංවෘත පද්ධතියක් තුළ සිදුවන ඕනෑම රසායනික ක්රියාවලියක දී ප්රතික්රියකවල ස්කන්ධය, ඵලවල ස්කන්ධයට සමාන විය යුතු බවයි.
පදාර්ථ සංස්ථිති නියමය (අංශුවල සංස්ථිතික බව හැගවෙන) විශේෂ සාපේක්ෂතාවාදය හා ක්වොන්ටම් යාන්ත්රණය පැමිණීමට පෙර තිබු දළ භෞතික විද්යාත්මක නීතියක් ලෙස සැලකිය හැක. විවිධ ශක්ති ස්වරූප පද්ධති තුළට හා පද්ධතියෙන් ඉවතට යන පරිදි ඇති විවෘත පද්ධතිවල දී ස්කන්ධය ද සංස්ථිතික නොවේ. කෙසේ වුවත් සංවෘත පද්ධති සදහා ස්කන්ධ සංස්ථිති නියමය ඒවායේ ගම්යතා කේන්ද්ර අවස්ථිතික රාමුවල අනුසාරයෙන් බැලූ විට නුතන භෞතික විද්යාවට අයත් වෙයි.
මෙම ඓතිහාසික සිද්ධාන්තය, රසායන විද්යාව, යාන්ත්ර විද්යාව හා තරල ගතිකය වැනි ක්ෂේත්රවල බහුලව යෙදේ.
ඉතිහාසය
[සංස්කරණය]

මෙම කොටස හිස්ය. එය පුළුල් කිරීමෙන් ඔබ හට උපකාර කළ හැක. |
ඓතිහාසික වැදගත්කම හා දියුණුව
[සංස්කරණය]මුල් කාලීන නමුත් අසම්පූර්ණ ස්කන්ධ සංස්ථිතිය පිළිබඳ නියමයන් 13 වන සියවසේ දී Nasīr al - Dīn al - Tūsī (1201 – 1274) විසින් ආරම්භ කරන ලදී. වස්තුවක් වෙනස් කළ හැකි මුත් අතුරුදහන් කළ නොහැකි බව ඔහු විසින් ප්රකාශ කරන ලදී.
1789 දී ස්කන්ධ සංස්ථිති නියමය මුල්වරට පැහැදිලිව ප්රකාශයට පත් කළේ (ඒ හේතුව නිසාම රසායන විද්යාවේ පියා ලෙස හඳුන්වන)ලැවොෂියර් (1734 – 1794) විසිනි. කෙසේ වුවත් 1748 දී මික්ලේයිල් ලොමොනොසොව් (1711 – 1765) විසින් මීට සමාන අදහසක් ප්රකාශයට පත් කර පර්යේෂණ මගින් සනාථ කර තිබිණි. ලැවොෂියර්ගේ කාර්යට දායක වූ අනෙක් අය අතරට ජෝසප් බ්ලැක් (1728 – 1799) හෙන්රි කැවෙන්ඩිෂ් (1731 – 1810) හා ජීන් රේ (1583 -1645) ඇතුළත් වේ.
ඓතිහාසිකව , වායුවල බර තරාදි මගින් මැනනු ලැබූ බවට ප්රකාශයට පත් කළ රික්තක පොම්පය සොයාගැනීමට පෙර තේරුම් ගැනීමට නොහැකිව තිබූ වායුවල බර කෙරෙහි පෘථිවි වායු ගෝලය මගින් ඇති කරන උත්ප්ලාවකතා බලපෑම නිසා ස්කන්ධ සංස්ථිතිය අපැහැලිව පැවතුණි. හඳුනාගත් පසු ඇල්කෙමි රසායන විද්යාව නූතන රසායන විද්යාව බවට පරිවර්තනය වීම සඳහා මෙම ස්කන්ධය හා සම්බන්ධ සංසිද්ධිය ඉවහල් වුනි. රසායනික ද්රව්ය කිසිලෙසක අතුරුදහන් නොවන බව විද්යාඥයන් තේරුම් ගත් විට තුලා පාඨාංක අනුව උත්පාලකතාව ද සැලකිල්ලට ගත් පසු ඔවුන්ට මුල්වරට රසායනික ද්රව්ය පරිවර්තනය වීම පිළිබදව ප්රමාණාත්මකව හැදෑරිය හැකි විය. මෙය මුලද්රව්ය පිළිබද මෙන්ම සියළුම රසායනික ක්රියා හා පරිවර්තන (දහනය හා පරිවෘත්තීය ඇතුළුව) , මූලද්රව්යවල විවිධ ද්රාවණ / බර අතර සරළ ප්රතික්රියාවක් යන අදහස ද ඇති වීමට මග පාදන ලදී. මෙම නියමය ලොව පුරා විද්යාඥයන් විසින් භාවිතයට ගනී.
ව්යාපනය
[සංස්කරණය]ස්කන්ධ සංස්ථිතිය විශේෂ සාපේක්ෂතාවෙය්දී නොගැළපේ
අංශු පද්ධතියක ස්කන්ධය එම අංශුවල ස්කන්ධවල එකතුවට සමාන වේ යන නියමය ආදී භෞතික විද්යාවේදී සත්ය වුවත් විශේෂ සාපේක්ෂතාවයේදී එසේ නොවේ. ස්කන්ධ ශක්ති සමතුල්යතා සමීකරණය බන්ධිත පද්ධතියක් ඒවායේ කොටස්වල එකතුවට වඩා අඩු ස්කන්ධයක් දක්වන බව හගවයි. එම වෙනස ස්කන්ධ දෝශය ලෙස හදුන්වන අතර එය බන්ධන ශක්තිය - කොටස් එකට තබා ගන්නා බන්ධනයේ ශක්තියයි. (වෙනත් ආකාරයකට ප්රකාශ කරනවා නම් ඒවා වෙන් කිරීමට ශක්තිය අවශ්යය.) ස්කන්ධ දෝශය ඉහළ යන තරමටම බන්ධන ශක්තිය ද වැඩිවේ. බන්ධිත පද්ධතියක් නිර්මාණය කිරීමට කොටස් එකතුවන විට බන්ධන ශක්තිය නිදහස් වේ. පද්ධතියෙන් ශක්තිය පිටවන විට ස්කන්ධය අඩුවේ.
ස්කන්ධ සංස්ථිතිය, ශක්තිය හා ගම්යතාව සංයුක්තකරණය වූ පද්ධතියක සංස්ථිතිය ලෙසද ප්රකාශ කළ හැක. එමගින් ද ඕනෑම පද්ධතියක් (ද්වි ෆෝටෝන පද්ධතිය මැන) ඕනෑම නිරීක්ෂකයෙක් සදහා සමාන නොවෙනස් ස්කන්ධයම ලබාදේ.
යුගල නිෂ්පාදනයෙන් නිර්මාණය කරන ලද අංශු සඳහා ද ස්කන්ධ සංස්ථිතිය අදාල වේ. සංවෘත පද්ධතියක නිත්ය ස්කන්ධය නව අංශු නිර්මාණය වූ විට වෙනස් නොවේ. සංවෘත පද්ධතියක පද්ධතිය තුළ කුමක් සිදු වුවත් සම්බන්ධවන ඒවායේ ස්කන්ධ නොවෙනස්ව පවතී.
ආශ්රිත
[සංස්කරණය]- Charge conservation
- Conservation law
- Fick's laws of diffusion
- Law of definite proportions
- Law of multiple proportions
මූලාශ්ර
[සංස්කරණය]- ^ Volkenstein, Mikhail V. (2009). Entropy and Information (illustrated ed.). Springer Science & Business Media. p. 20. ISBN 978-3-0346-0078-1. Extract of page 20
- ^ Okuň, Lev Borisovič (2009). Energy and Mass in Relativity Theory. World Scientific. p. 253. ISBN 978-981-281-412-8. Extract of page 253
- ^ Lewis, David (2012). Early Russian Organic Chemists and Their Legacy (illustrated ed.). Springer Science & Business Media. p. 29. ISBN 978-3-642-28219-5. Extract of page 29
