සමාන්තර පරිගණනය

සමාන්තර පරිගණනය (Parallel Computing) යනු පරිගණක ආශ්‍රිත ගණනය කිරීම් විශාල සංඛ්‍යාවක් එකවිට එකිනෙකට සමාන්තරව දියත් කිරීමයි.^[1]. විශාල සහ සංකීර්ණ ප්‍රශ්නයක් කුඩා කොටස් වලට වෙන්කර ඒවා වෙන වෙනම සහ සමාන්තරව එක විට ගණනය කිරීම මගින් විසදා ගැනීම මෙහි ප්‍රධාන මූලධර්මයයි. සමාන්තර පරිගණනයේ ප්‍රභේද කීපයකි. ඒවා නම් බිටු මට්ටම (bit level), විධාන මට්ටම (instruction level), දත්ත (data) සහ ක්‍රියා අනුවර්තී වාදයයි (task parallelism). ක්‍රියා අනුවර්තී වාදය දැනට බොහෝ කලක සිට භාවිතයේ තිබුනද එය ප්‍රධාන වශයෙන් යොදා ගැනුනේ අධි ක්‍රියාකාරි පරිගණක (high-performance computing) සදහා පමණි. එහෙත් පසුකලක එහි භාවිතය වර්ධනය වන්නට වූයේ සංඛ්‍යාත පරිමාණනය (frequency scaling) සදහා භෞතික සීමා ඇතිවූ බැවිනි^[2]. පරිගණක සදහා වැය වන ශක්ති ප්‍රමාණය (ඒ නිසා ජනනය වන තාපය) මෑත කාලීනව විශාල ලෙස සැලකිල්ලට ලක්වූ නිසා^[3] සමාන්තර පරිගණනය පරිගණක නිර්මාණ ශිල්පයේ සහ විශේෂයෙන්ම බහු හර දත්ත සකසන (multicore processor) සදහා ප්‍රමුඛතම න්‍යායක් බවට පත්විය^[4].

සමාන්තර පරිගණකවල දෘඩාංග, ක්‍රියා අනුවර්තීතාවය සදහා සහය දක්වන මට්ටම අනුව දළ ලෙස වර්ග කළහැක. පළමු වැන්න නම් බහු හර (milti-core) සහ බහු දත්ත සැකසුම් (multi-processor) ඒකක වැනි බහු දත්ත සැකසුම් මූලාශ්‍ර එක්කොට තනාඇති තනි පරිගණක වේ. දෙවැන්න නම් පොකුරු පරිගණක (clusters), විශාල ප්‍රමාණයේ සමාන්තර පරිගණනය (Massive parallel processing) සහ කොට්ටාශ පරිගණනය (grid computing) වැනි පරිගණන උපාංග රාශියක් එක්කොට තැනූ ප්‍රභල පරිගණක යන්ත්‍ර වේ. මීට අමතරව සමහර සාමාන්‍ය පරිගණන කටයුතු වේගවත්ව සිදුකරගැනීම සදහා සාම්ප්‍රදායික පරිගණක සමග විශේෂිත සමාන්තර පරිගණන නිර්මාණශිල්ප එක්කර ක්‍රීයාත්මක කිරීමද සිදුකරයි.

සමාන්තර පරිගණන වැඩසටහන් ලිවීම සාමාන්‍ය අනුක්‍රමික වැඩසටහන් ලිවීමට වඩා ඉතා අපහසු වේ^[5]. මෙයට හේතුව නම් සමාන්තර පරිගණනයේදී වියහැකි මෘදුකාංග දෝෂ කීපයක් හදුනාගෙන ඇති බැවිනි. උදාහරණයක් ලෙස තරඟකාරී තත්ත්වය (race condition) දැක්විය හැක. වෙන් කරන ලද කුඩා වැඩසටහන් කොටස්වල සන්නිවේදනය සහ සමමුහුර්තකරණය නිවැරදිව ඉටුකිරීම හොද සමාන්තර පරිගණන වැඩසටහනක් ලිවීමේ ප්‍රධාන අභියෝගය වේ.

සමාන්තර පරිගණනය සදහා ලියන ලද වැඩසටහනක ලබාගතහැකි උපරිම වේගය අම්ඩාල් (Amdahl) ගේ නියමයට අනුකූල වේ.

පසුබිම

සාමාන්‍යයෙන් පරිගණක වැඩසටහන් ලියනු ලබන්නේ ශ්‍රේණිගත (Serial) ආකාරයෙනි. ගණිත ගැටලුවක් විසදීම සදහා ඇල්ගොරිතම ලියනු ලබන්නේ ශ්‍රේණිගතව ගලායන විධාන (Instruction) මාලාවක් ලෙසිනි. මෙම විධාන පරිගණකයේ මධ්‍යම සැකසුම් ඒකකයේදී (Central Processing Unit) සකසනු ලබයි. මෙහිදී එකවිට එක් විධානයක් පමණක් සකසනු ලබන අතර එය නිම වූ පසු අනෙක් විධානය සැලකිල්ලට ගනී^[6]. අනෙක් අතට ගත්විට සමාන්තර පරිගණනයේදි සිදුවන්නේ විධාන මාලාවක් සමාන්තරව එකවර විසදීමයි. මෙය සිදුකරනු ලබන්නේ මූලික ප්‍රශ්නයෙහි කුඩා කොටස් වෙන්කර එම වෙන් වෙන් කොටස් එකවර අනෙක් සමගාමී කොටස් ද සමග සැකසීමයි. මේ සදහා යොදාගන්න සැකසුම් මූලිකාංග විවිධාකාර වියහැකි අතර බහු දත්ත සැකසුම් ඒකක සහිත තනි පරිගණක, ජාලගත කරනලද පරිගණක, විශේෂිත දෘඩාංග හෝ මේවායින් එකවර කීපයක් යොදා ගතහැකිය.

පරිගණකවල ප්‍රබලතාවය වැඩිකරගැනීම උදෙසා 1980 මැද භාගයේ සිට 2004 දක්වා වූ කාලයේදී ප්‍රමුඛ වූ ප්‍රධානතම සංකල්පය වූයේ සංඛ්‍යාත පරිමාණනයයි (Frequency scaling). පරිගණක වැඩසටහනක ධාවන කාලය (Runtime) එහි විධාන සං‍ඛ්‍යාවේ සහ එක විධානයක් සැකසීම සදහා ගතවන මධ්‍යන්‍ය කාලයෙහි ගුණිතයක් ලෙස සැලකේ. අනෙක් සියලු කරුණු නියතයක් ලෙස ගත් විට මධ්‍යම සැකසුම් ඒකකයේ සංඛ්‍යාතය වැඩි කරන විට ඒකක කාලයකදී සකස් කළහැකි විධාන ප්‍රමාණයද ඉහළ යයි. මේ නිසා සංඛ්‍යාතය වැඩිකිරීම මගින් පරිගණක වැඩසටහනක ධාවන කාල අඩුකරගතහැකිය. මෙය සියළුම පරිගණක සම්බන්ද වැඩසටහන් සදහා සත්‍ය වේ^[7].

කෙසේ උවද පරිගණක චිපයක ශක්ති පරිභෝජනය සදහා සමීකරණය සලකා බලන්න. P = C × V2 × F මෙහි P යනු ශක්තියද C යනු කාල චක්‍රයකදී වෙනස්වන ධාරිතාවයද (Capacitance) වේ. V යනු වෝල්ටීයතාවද (Voltage) F යනු දත්ත සකසනයේ සංඛ්‍යාතයද ( තප්පරයට චලන) වේ^[8]. මෙහි ආකාරයට දත්ත සකසනයක සංඛ්‍යාතය වැඩිකිරීම නිසා එය භාවිතා කරන ශක්ති ප්‍රමාණයද ඉහළ යයි. මෙසේ අධික ලෙස ශක්ති පරිභෝජනය කරන දත්ත සකසන කීපයක් 2004 වර්ශයේදී Intel සමාගම විසින් අත්හිටවනු ලැබීය. මෙසේ අත්හිටවනු ලැබූ Tejas සහ Jayhawk දත්ත සකසන සමගම ශක්ති පරිභෝජනය වැඩී කිරීම මගින් සංඛ්‍යාතය වැඩි කර පරිගණක වැටසටහන් වේගවත් කිරීමේ ක්‍රියාවලියද අවසන් විය^[9].

මූවර් ගේ නියමය (Moore's Law) යනු පරීක්ශණ සහ නිරීක්ශණ පාදක කරගෙන ඉදිරිපත් කරනලද සුප්‍රකට න්‍යායකි. එයින් කියවෙන්නේ සෑම මාස 18 ත් 24 ත් අතර කාලයකදී පරිගණක චිපයක අඩංගු කළහැකි ට්‍රාන්සිස්ටර ප්‍රමාණය දෙගුණයකින් ඉහළ යන බවයි^[10]. ශක්ති පරිභෝජනය සම්බන්දව ඉහත කීලෙස විවිධ ගැටලු ඇති වුවද 70 දශකයේදී ඉදිරිපත් කරනලද මුවර්ගේ නීතිය තවමත් එලෙසින්ම නොබිදී පවතී. සංඛ්‍යාත පරිමාණන සංකල්පය බිඳවැටීමත් සමගම දත්ත සැකසුම් ඒකක සදහා අළුතෙන් එක්කරන ට්‍රාන්සිස්ටර යොදා ගැනෙනුයේ සමාන්තර පරිගණනය සදහා අවශ්‍ය නව දෘඩාංග පරිගණක චිප වලට එක් කිරීම සදහායි.

අම්ඩාල් (Amdahl)ගේ නීතිය සහ ගුස්ටැෆ්සන් (Gustafson)ගේ නීතිය

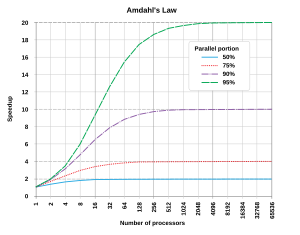
ආම්ඩාල් ගේ නීතිය (Amdahl's Law) ප්‍රස්ථාරික නිරූපණය. යම් වැඩසටහනක් කොපමන ප්‍රමාණයකින් සමාන්තරගත කළහැකිද යන්න අනුව එම වැඩසටහන සමාන්තර පරිගණනය මගින් කොපමණ වේගවත් කළහැකිද යන්න තීරණය වේ. උදාහරණයක් ලෙස යම් වැඩසටහනක් 90% කින් සමාන්තරගත කළහැකි නම් , සමාන්තරගත කළ නොහැකි වැඩසටහන් කොටස 10% නම් , එම වැඩසටහන වේගවත් කළහැකි උපරිමය කොපමන දත්ත සකසන ප්‍රමාණයක් භාවිතා කළද දස ගුණයකට වඩා වැඩි නොවේ.

පරිගණන සමාන්තරකරණය මගින් දත්ත සැකසීම වේගවත් කිරීමේ ක්‍රමයක් ලෙස දත්ත සකසන ඒකක ගණන දෙගුණ කිරීම මගින් වැඩසටහන් ධාවන කාලය අඩකින් අඩුකිරීම දැක්වියහැක. නැවත වාරයක් එසේ දෙගුණ කිරීම මගින් නැවතත් ධාවන කාලය අඩකින් අඩු කළහැකිය. එනම් රේඛීය (linear) ලෙස වේගවත් බව වැඩි කරගත හැකිය. කෙසේ නමුත් මෙසේ ප්‍රශස්ත මට්ටමකට වේගවත් කළහැකි වන්නේ සමාන්තර ඇල්ගොරිතම කීපයක් පමණි. බොහෝ ඇල්ගොරිතම මගින් ආසන්න ලෙස හෝ රේඛීය තත්ත්වයෙන් වේගවත් කිරීම් සිදුකරනු ලබන්නේ දත්ත සැකසුම් මූලිකාංග කීපයක් සදහා පමණි. ඉන්පසු දත්ත සැකසුම් මූලිකාංග ඒකක ප්‍රමාණය ඉහළ යත්ම එම රේඛීය භාවය කෙමෙන් ඒකාකාරී තත්වයකට පත්වේ.

සමාන්තර පරිගණන වේදිකාව (parallel computing platform) සදහා විභව වේගවත් කිරීමේ සමීකරණය අම්ඩාල්ගේ නීතියයි. එය සූත්‍රකෘත කරනු ලැබූයේ 1960 දීයි^[11]. එමගින් කියවෙන ආකාරය අනුව ප්‍රධාන වැඩසටහනෙහි අඩංගු කුඩා සමාන්තරකරණය කළ නොහැකි කොටසක් නිසා සම්පූර්ණ වැඩසටහනේම වේගවත් කිරීම අඩාලවේ. විශාල ගණිතමය හෝ ඉන්ජිනේරුමය ගැටලුවක් විසදීම සදහා ලියනලද පරිගණක වැඩසටහන් වල සමාන්තරීකරණය කළහැකි වැඩසටහන් කොටස් මෙන්ම එසේ කළ නොහැකි කොටස් ද අඩංගු වේ. මෙසේ සමාන්තරගත කළනැහැකි කුඩා වැඩසටහනෙහි ධාවන කාල භාගය α නම් , එවිට

S={\frac {1}{\alpha }}

මගින් ලබාදෙනුයේ එම වැඩසටහනේ උපරිම සමාන්තරගතකරණ වේගයයි. වැඩසටහන සදහා අනුක්‍රමික කොටස 10% නම් එම වැඩසටහන සදහා ලබාගතහැකි වේගවත් බව දස ගුණයකට (‍x10) වඩා වැඩි කරගත නොහැක. එනම් ඉන්පසු කොපමන දත්ත සැකසුම් ඒකක තව තවත් එක්කලද ප්‍රතිඵලය එකම වේ. ඒ නිසා සමාන්තරගතව දත්ත සැකසුම් මූලිකාංග එක්කළ හැකි උපරිමයක් ඇත.

ගුස්ටැෆ්සන් (Gustafson)ගේ නීතිය තවත් පරිගණනය සම්බන්ද නීතියකි. මෙය අම්ඩාල්ගේ නිතිය හා සමීපව සම්බන්ද වේ^[12]. එයින් කියවෙන පරිදි $P$ සංඛ්‍යාවක් දත්ත සැකසුම් ඒකක සමග වැඩසටහනක් වේගවත් කිරීමේදී

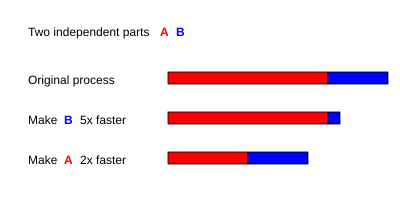
යම් නියමිත කර්ත්ව්‍යයක් සදහා එකිනෙකට වෙනස් අනුකොටස් දෙකක් ඇතැයි සිතන්න. ඒවා A සහ B ලෙස ගනිමු. සම්පූර්ණ පරිගණනයෙන් B වල කොටස 25%කි. පරිගණක ක්‍රමලේඛන සම්පාදකයෙකුට (programmer) මෙම කොටස පස් ගුණයකින් වේගවත් කළහැක, එහෙත් ඉන් මුළු වැඩසටහන වේගවත් වන්නේ ඉතා කෙටි කලකින් පමණි(රූපය). එම නිසා වැඩසටහන වේගවත් කිරීමට නම් A කොටස දෙගුණයක් වේගවත් කළයුතුය. එය B වේගවත් කිරීමට වඩා බෙහෙවින් ඵලදායි වේ.

S(P)=P-\alpha (P-1).\,

අම්ඩාල්ගේ නීතියේ ආකාරයට අනුව ගන්නා උපකල්පනයක් නම් වැඩසටහනේ සමාන්තරගත කළ නොහැකි අනුක්‍රමික කොටසෙහි ධාවන කාලය, යොදා ගන්නා දත්ත සැකසුම් සංඛ්‍යාවෙන් ස්වාධීනය යන්නයි. එහෙත් මෙම උපකල්පනය ගුස්ටැෆ්සන්ගේ නීතියෙහි භාවිතා නොවේ.

පරායත්තතාව (Dependencies)

සමාන්තර පරිගණනය සදහා ඇල්ගොරිතම (parallel algorithms) සකස් කිරීමේදී අවශ්‍ය මූලික කරුණක් ලෙස දත්ත පරායත්තතාවය (data dependencies) අවබෝද කරගැනීම දැක්වියහැක. කිසිම වැඩසටහනකට තම දීර්ඝතම පරායත්ත ගණනය කිරීම් ශ්‍රේණියට වඩා වේගවත්ව වැඩසටහන නිමා කළ නොහැක (Critical path method). කුමක් නිසාදයත් අනිත් ගණනය කිරීම් මත යැපෙන ගණනයකිරීම් පිළිවෙලින් එකිනෙක කළයුතු බැවිනි. එහෙත් බොහෝ ඇල්ගොරිතම වල මෙසේ එකිනෙකට දීර්ඝ ලෙස සම්බන්දිත ගණනය කිරීම් නොමැති නිසා ඒවා සමාන්තර ලෙස වෙන වෙනම ගණනය කළහැක.

P_i සහ P_j වැඩසටහනක කොටස් දෙකක් ලෙස ගනිමු. මේවා බර්න්ස්ටගේ කොන්දේසි ^[13] (Bernstein's conditions) වලට අනුකූල වන්නේ එකිනෙකට ස්වාධීන හා සමාන්තරව ගණනය කළහැකිනම් පමණි. P_i, නම් I_i යනු සියලු ප්‍රධාන විචල්‍යයන්ද O_i යනු ප්‍රතිදානවේ. ඒ ආකරයෙන්ම P_j, P _i සහ P_j එකිනෙකට ස්වාධීනවේ.

$I_{j}\cap O_{i}=\varnothing ,\,$
$I_{i}\cap O_{j}=\varnothing ,\,$
$O_{i}\cap O_{j}=\varnothing .\,$

මෙහි පළමු කොන්දේසිය උල්ලංගනය කිරීම නිසා ප්‍රවාහ පරායත්තතාවය ඇතිවේ (flow dependency). පළමු ප්‍රකාශයේ පිළිතුරු දෙවැන්න මගින් භාවිතා කරයි. දෙවන ප්‍රකාශයෙන් ප්‍රති-පරායත්තතාවක් පෙන්නුම් කරයි. තුන්වන සහ අවසන් ප්‍රකාශයෙන් පෙන්වාදෙන්නේ ප්‍රතිදාන පරායත්තතාවයි. මෙම ප්‍රකාශ දෙක එකම ස්ථානයක සදහන් කළවිට අවසන් ප්‍රතිඵල ලැබිය යුත්තේ තර්කානුකූලව අවසානයේ සකසනය වූ ප්‍රකාශයයි.

පහත දැක්වෙන සමීකරණය බලන්න, එමගින් විවිධ වූ පරායත්තතාවන් ආදර්ශනයකරයි.

1: function Dep(a, b)
2:    c := a·b
3:    d := 3·c
4: end function

මෙහි තුන්වන කණ්ඩය දෙස බලන්න, එය දෙවන කණ්ඩය නොමැතිව ගණනය කළනොහැක (සමාන්තරව වුවද කළ නොහැක), එයට හේතුව නම් දෙවන කණ්ඩයේ පිළිතුර තුන්වන කණ්ඩය සදහා අත්‍යාවශ්‍ය බැවිනි. එනම් එය ඉහත සදහන් කළ පළමු කොන්දේසිය උල්ලංගනය කරමින් ප්‍රවාහ පරායත්තතාවය ඇතිකරයි (flow dependency).

1: function NoDep(a, b)
2:      c := a·b
3:      d := 3·b
4:      e := a+b
5: end function

මෙම උදාහරණයේදී කිසිදු පරායත්තතාවක් නොමැති නිසා මේවා සියල්ල එකවිට සමාන්තරව ගණනය කළහැක. බර්න්ස්ටෙන්ගේ කොන්දේසි අනුව දත්ත සකසන අතර මතකය හවුලේ බෙදාගැනීමක් සිදු නොකරයි. එහෙත් සමහර අවස්ථා වලදී එසේ බෙදාහැරීම වැදගත් වේ. උදාහරණ: semaphore (programming), barrier (computer science) සහ Synchronization (computer science) වැනි අවස්ථා.

තරඟකාරී තත්වය (Race conditions), පොදු බැහැර කිරීම (Mutual Exclusion), සමමුහුර්තකරණය (Synchronization) සහ සමාන්තර අඩපනවීම (Parallel Slowdown)

සමාන්තර පරිගණන වැඩසටහනක ඇති අනුකොටස් බොහෝ විට නූල් / Thread (computer science) නමින් හදුන්වයි. සමහර පරිගණක වැඩසටහන් මගින් ඊටත් වඩා කුඩා ඒකක වන තන්තු / Fiber (computer science) යොදාගනී. අනෙක් වැඩසටහන් වඩාත් විශාල අනු කොටස් වල්ගයක් වන සකසන Process (computing) යොදාගනී. එහෙත් බොහෝවිට සම්මතයක් ලෙස පරිගණක වැඩසටහන් වල අනුකොටස් ලෙස පිළිගන්නේ නූල් / thread ආකාරයෙනි. මෙම නූල් නිතරම ඒවා එකිනෙක හවුලේ තබාගන්නා විචල්‍ය / variable (programming) යාවත්කාලීන කිරීම සිදුකරයි. වැඩසටහන් දෙකක් අතර විධාන පහත ආකාරයෙන් විවිධ පිළිවෙලින් තිබියහැක.

Thread A	Thread B
1A: Read variable V	1B: Read variable V
2A: Add 1 to variable V	2B: Add 1 to variable V
3A Write back to variable V	3B: Write back to variable V

1B විධානය 1A සහ 3A අතරදී දත්ත සැකසුවහොත් හෝ 1A විධානය 1B සහ 3B අතර දත්ත සකස් කළහොත් වැඩසටහන වැරදි දත්ත නිපදවයි. මෙය තරඟකාරී තත්වය (Race conditions) නමින් හැදින්වේ. වැඩසටහන් ක්‍රමලේඛකයා විසින් අනිවාර්යයෙන් අගුලක් / Lock (computer science) මේ සදහා සකස්කළ යුතුවේ. එමහින් පොදු බැහැර කිරීමක් (Mutual Exclusion) සිදුවේ. මෙසේ අගුලක් / lock යනු ක්‍රමලේඛන භාෂා ඉදිකිරීමක් වන අතර එමගින් එක් නූලකට පමණක් විචල්‍යයක පාලනය සියතට ගෙන අනෙක් නූල් වලට එම විචල්‍යය කියවීම හෝ ලිවීමෙන් වලක්වා එය අගුල් දැමීමක් සිදුකරයි. මේ එවැනි අගුල් භාවිතා කර නැවත ලියනලද වැඩසටහනයි.

Thread A	Thread B
1A: Lock variable V	1B: Lock variable V
2A: Read variable V	2B: Read variable V
3A: Add 1 to variable V	3B: Add 1 to variable V
4A Write back to variable V	4B: Write back to variable V
5A: Unlock variable V	5B: Unlock variable V

මෙහිදී එක් නූලක් පමණක් සාර්ථකව විචල්‍ය V අගුලුලාගනී. අනෙක් නූල මෙහිදී ක්‍රියා විරහිත වන අතර එයට V විචල්‍යය නැවත අගුලු අරිනතුරු කියවීම හෝ ලිවීම කළ නොහැක. මෙම ක්‍රමය නිවැරදි වැඩසටහන් ක්‍රියාකාරීත්වයක් සදහා උදවු වුවද වැඩසටහන බෙහෙවින් මන්දගාමී කළහැක.

මෙවැනි විචල්‍යයන් කීපයක් එකවර අගුලුලෑම සදහා යොදාගන්නා පරමාණුක නොවන (Atomic operation) වැඩසටහනක් සම්පූර්ණයෙන් ඇනහිටීමක් උවද වියහැක (deadlock). පරමාණුක අගුලුලෑමක් මගින් එකවර විචල්‍ය කීපයක් අගුලු ලෑම කළහැකි අතර එකදු විචල්‍යයක් හෝ එසේ අගුලු ලෑම කළනොහැකි නම් එය කිසිදු විචල්‍යයක් අගුලු ලෑමෙන් වැලකී සිටියි. මෙවැනි අවස්ථාවකදී නූලට තම කටයුතු සම්පූර්ණ කළනොහැකි නිසා සම්පූර්ණ වැඩසටහනම අඩපණ වේ.

බොහෝ සමාන්තර පරිගණන වැඩසටහන් සදහා ඒවායේ අනුකොටස් සමමුහුර්තකරණය අවශ්‍යවේ. මෙහිදී පරිගණන බාදකයක් (barrier) යෙදවීම කළයුතු වේ. මෙම බාදක බොහෝ විට මෘදුකාංග අගුලු භාවිතයෙන් ස්ථාපනය කරයි.

සියළුම සමාන්තරකරණයන් මගින් වේගවත් බව ලැබෙන්නේද නැත. සාමාන්‍යයෙන් යම් කාර්යයක් කොටස් වලට බෙදා වෙන්කළ විට ඒවා එකිනෙක සන්නිවේදනයේදී යොදාගන්නා කාලයද ඉහළ යයි. මේ නිසා සමහර අවස්ථා වලදී ගැටලු විසදීමට ගතවන කාලයට වඩා වැඩි කාලයක් මෙසේ සන්නිවේදන කටයුතු සදහා වැයවියහැක. මෙසේ අතිරේක සමාන්තරකරණය නිසා වැඩසටහන් වල සිදුවන අඩපනවීම සමාන්තර අඩපනවීම නමින් හදුන්වයි (Parallel Slowdown).

මෘදු මුහුණත (Fine-grained), රළු මුහුණත (coarse-grained) සහ අපහසුතා සමාන්තරකරණය (embarrassing parallelism)

පරිගණක වැඩසටහන් බොහෝ විට ඒවායේ අනුකොටස් එකිනෙක සමමුහුර්තකරණය කිරීම කොතරම් ඉක්මනින් කළයුතුද යන්න අනුව වර්ගීකරණය කරයි. මෘදු මුහුණත (Fine-grained) වර්ගයේ වැඩසටහන් වල අනුකොටස් අතර තප්පරයකට කීපවරක් සමමුහුර්ත කිරීම් කළයුතු අතර රළු මුහුණත (coarse-grained) වර්ගයේ වැඩසටහන් සදහා එසේ තප්පරයකට කීපවරක් සමමුහුර්තකරණය අවශ්‍ය නොවේ. අපහසුතා සමාන්තරකරණය (embarrassing parallelism) වර්ගයේ වැඩසටහන් ඉතා කලාතුරකින් සමමුහුර්තකරණය කරන අතර සමහරවිට එසේ කිරීමක් කිසිවිටෙකවත් අවශ්‍ය නොවේ.

සංස්ථිතික ආකෘති (Consistency models)

සමාන්තර පරිගණනය සදහා යොදා ගන්නා ක්‍රමලේඛන භාෂා සහ දෘඩාංග සදහා සංස්ථිතික ආකෘතියක් තිබීම වැදගත් වේ. මෙම ආකෘතිය මගින් පරිගණක මතකය මෙහෙයවිය යුතු ආකාරය පිළිබඳව සහ ප්‍රතිඵල දියයුතු ආකාරය පිළිබඳව නීති සහ කොන්දේසි සකසයි.

සංස්ථිතික ආකෘති අතර මුලින්ම පැමිණි ආකෘති වලින් එකක් ලෙස ලෙස්ලි ලැම්පෝර්ට්ගේ (Leslie Lamport) අනුක්‍රමික සංස්ථිතික ආකෘතිය (sequential consistency) හැදින්විය හැක. අනුක්‍රමික සංස්ථිතිය යනු සමාන්තර පරිගණන වැඩසටහනක කොටසක් වන අතර එමගින් ලැබෙන ප්‍රතිඵල අනුක්‍රමික පරිගණක වැඩසටහනක ප්‍රතිඵල වලට සමාන වේ^[14].

මෘදුකාංග ගණුදෙණුකාර මතකය යනු සංස්ථිතික ආකෘතියෙහි බහුලව භාවිතාවන අකාරයකි. මෘදුකාංග ගණුදෙණුකාර මතකය මගින් දත්ත කළමනාකරණ පද්දතියෙන් (Database management system) තාවකාලිකව තොරතුරු ලබාගනී. මෙසේ තොරතුරු/ දත්ත ලබාගැනීම සදහා පරමාණුක ගනුදෙනු (atomic transactions) සදහා වූ සංකල්පය යොදාගනී.

ෆ්ලින්ගේ වර්ගීකරනය (Flynn's taxonomy)

සමාන්තර පරිගණක සහ අනුක්‍රමික පරිගණක සදහා මුලින්ම වර්ගීකරණයක් ඉදිරිපත් කරනලද්දේ මයිකල් ෆ්ලින් (Michael J. Flynn) විසිනි. එය ෆ්ලින්ගේ වර්ගීකරණය නමින් හැදින්වේ. ඔහු ඒවා වර්ගීකරනය කරන ලද්දේ ඒවා භාවිතයට ගන්නා විධාන ගණන අනුවයි. එනම් එම විධාන භාවිත කරන්නේ ඒකීය දත්ත කට්ටලද නැතහොත් බහු දත්ත කට්ටලද යන්න මතයි.

v
t
e

**Flynn's taxonomy**
	Single instruction	Multiple instruction
Single data	SISD	MISD
Multiple data	SIMD	MIMD

The single-instruction-single-data (SISD) යන වර්ගීකරණය අදාල වන්නේ මුල් කාලීන අනුක්‍රමික වැඩසටහන් සදහායි. The single-instruction-multiple-data (SIMD) වර්ගීකරණය අනුව එකම මෙහෙයුමක් පුන පුනා භාවිතයෙන් විශාල දත්ත ප්‍රමාණයක් සකසනය කිරීම මෙහිදී සිදුවේ. මේවා බහුලව භාවිතා වන්නේ ඒකීය සැකසුම් (signal processing) වැඩසටහන් වලයි. Multiple-instruction-single-data (MISD) යනු ඉතා කළාතුරකින් යොදාගන්නා වර්ගීකරණයක් වන අතර වැඩසටහන් කීපයක් මගින් පමණක් මෙය යොදාගනී. Multiple-instruction-multiple-data (MIMD) යන වැඩසටහන් සමාන්තර පරිගණනයේ බහුලවම යෙදෙන වැඩසටහන් වර්ගය වේ.

අනුවර්තී වාදයේ ප්‍රභේද

බිටු මට්ටමේ අනුවර්තී වාදය (Bit-level parallelism)

1970 සිට 1986 වනතෙක් කාලය තුළ VLSI (very-large-scale integration) පරිගණක චිප වල පැමිණීමත් සමග පරිගණක නිර්මාණශිල්පයේ දියුණු වීම පරිගණක වචන විශාලත්වය (computer word size) දෙගුණ කිරීම මත තීරණය විය^[15]. එනම් දත්ත සකසනයකට එක් චක්‍රයක් සදහා මෙහෙයවිය හැකි තොරතුරු ප්‍රමාණය මත තීරණය විය. වචනයක විශාලත්වය වැඩි කිරීමත් සමග එමගින් දත්ත සකසනය මගින් පිළිපැදියයුතු උපදෙස් ප්‍රමාණය අඩු විය.

අතීතයේ සිට බිටු 4 (4-bit) ක්‍ෂුද්‍ර දත්ත සකසන බිටු 8 (8-bit) සහ බිටු 16ත් (16-bit)ඉන්පසු බිටු 32ත් (32-bit) භාවිතා කරන ක්‍ෂුද්‍ර දත්ත සකසනත් භාවිතයට පැමිණිනි. මෙම නැඹුරුව බිටු 32 ක්‍ෂුද්‍ර දත්ත සකසන හදුන්වාදීමත් සමග අවසන් විය. බිටු 32 වචන විශාලත්වය ඉන්පසු දශක දෙකක් තිස්සේම සම්මතයක් ලෙස පරිගණනයේදී භාවිත කළද මෑතකාලීනව පැමිණි බිටු 64 (64-bit) තාක්ෂණය (x86-64 architectures) මගින් බිටු 32 තාක්ෂණය අභිබවනු ලැබීය.

විධාන මට්ටමේ අනුවර්තී වාදය (Instruction level parallelism)

IF = Instruction Fetch/විධාන කැඳවීම, ID = Instruction Decode/විකේත කිරීම, EX = Execute/ක්‍රියාකාරී කරවීම, MEM = Memory access/මතකයට ඇතුලු කිරීම, WB = Register write back/නැවත ලිවීමයි)

පරිගණක වැඩසටහනක් යනු කෙටියෙන් ගත්කළ විධාන ධාරාවක් දත්ත සැකසුම් ඒකකයක් මගින් සකස් කිරීමයි. මෙම විධාන නැවත පෙලගැස්වීමත් එක් කිරීමත් කර ලැබෙන ප්‍රතිථල වල වෙනසකින් තොරව සමාන්තරව ක්‍රියාකරවීම විධාන මට්ටමේ අනුවර්තී වාදය ලෙස හැදින්වේ. 1980 දශකයේ මැද භාගයේ සිට 1990 දශකයේ මැදි භාගය දක්වා පරිගණක නිර්මාණශිල්පයේ කැපී පෙනෙන අංගයක් ලෙස මෙය හැදින්වියහැක^[16].

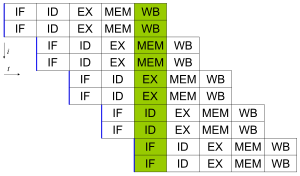
නවීන දත්ත සකසන සතුව අදියර කීපයකින් යුතු විධාන නල මාර්ග (instruction pipelines) දැකියහැක. මෙසේ ඇති සෑම අදියරකදීම දත්ත සකසනය මගින් කරන කාර්යය අදාල නල මාර්ගය අනුව වෙනස් වේ. N අදියරේ නල මාර්ග වලට N සං‍ඛ්‍යාවක් වෙනස් විධාන සමාප්තියේදී සටහන් කළහැක. මෙසේ නලමාර්ගකරනය සදහා හොදම උදාහරණයක් ලෙස RISC දත්ත සකසනය හැදින්වියහැක. මෙහි ක්‍රියාවලි අදියර 5 කින් යුතු විය. ඒවා නම් විධාන කැඳවීම, විකේත කිරීම, ක්‍රියාකාරී කරවීම, මතකයට ඇතුල් කිරීම සහ නැවත ලිවීමයි.(instruction fetch, decode, execute, memory access, and write back). පෙන්ටියම් 4 වර්ගයේ දත්ත සකසන වල මෙසේ පියවර 35 අඩංගු විය^[17].

අදියර 5ක නලමාර්ගික සුපිරි අදිශ දත්ත සකසන (superscalar) වලට එක් චක්‍රයක් සදහා විධාන දෙකක් නිකුත් කළහැක. මේ නිසා ඕනෑම අදියරකදී විධාන දෙකක් තිබියහැක. මෙලෙස විධාන 10 දක්වා එකවිට සකසනය කළහැක. නලමාර්ගකරණය මගින් මෙහෙයවන විධාන මට්ටමේ අනුවර්තී වාදයට අමතරව සමහර දත්ත සැකසුම් ඒකක වලට එකවරකට විධාන එකකට වඩා දියහැක. මේවා සුපිරි අදිශ දත්ත සකසන ලෙස හදුන්වයි. මෙහිදී දත්ත වල පරායත්තතාවක් (data dependency) නොමැති නම් විධාන කන්ඩායම් ගතකළහැක. මෙසේ අනුක්‍රමණයකින් තොර විධාන මට්ටමේ අනුවර්තී වාදය ගොඩනැගියහැකි බහුලව යොදා ගන්නා ක්‍රම ශිල්ප දෙකක් ලෙස Scoreboard සහ Tomasulo යන ඇල්ගොරිතම හැදින්වියහැක.

දත්ත අනුවර්තී වාදය (Data parallelism)

දත්ත අනුවර්තී වාදය යනු ලූප සහිත වැඩසටහන් සදහා වන සමාන්තරකරණයකි. මෙමගින් එකිනෙකට වෙනස් පරිගණන මාර්ග හරහා සමාන්තර දත්ත පරිවහනය ඉලක්ක කරයි. ලූප (program loops) සමාන්තරකරණය මගින් විශාල දත්ත ආකෘති සදහා එකිනෙකට සමාන මෙහෙයුම් අනුක්‍රමණ දියත් කිරීම සිදුකරයි. විශාල වශයෙන් විද්‍යාත්මක සහ ඉන්ජිනේරු වැඩසටහන් ඉදිරිපත් කිරීම සදහා දත්ත අනුවර්තී වාදය යොදාගනී^[18].

ලූපයක් මගින් ගෙනයනු ලබන පරායත්තතාවය යනු ලූපීය අනුශ්‍රේණියකක් පෙර ප්‍රතිඵල මත රදාපැවතීමයි. මේ නිසා ලූපයක් මගින් ගෙනයනු ලබන පරායත්තතාවය මගින් සමාන්තරකරණය අඩාල කරයි. පහත දැක්වෙන pseudocode දෙස බලන්න.

1:    PREV1 := 0
2:    PREV2 := 1
4:    do:
5:       CUR := PREV1 + PREV2
6:       PREV1 := PREV2
7:       PREV2 := CUR
8:    while (CUR < 10)

මෙම ලූපය සමාන්තරගත කළ නොහැක. එයට හේතුව නම් CUR , PREV2 සහ PREV1 මත රදා පවතින බැවිනි. මේ අයුරින් සෑම ප්‍රතිඵලයක්ම කලින් ප්‍රතිඵලය මත රදා පවතින නිසා මෙය සමාන්තරගත කළ නොහැක. මෙසේ ගැටලුවේ ප්‍රමාණය විශාල වන තරමට දත්ත අනුවර්තී වාදයද වැඩි වේ^[19].

ක්‍රියා අනුවර්තී වාදය (Task parallelism)

ක්‍රියා අනුවර්තී වාදය යනු සමාන්තර පරිගණන වැඩසටහනක දැකියහැකි ගති ලක්ෂණයකි. එයින් කියවෙන්නේ එකම හෝ වෙන වෙනස් දත්ත කට්ටලයක් භාවිතයෙන් එකිනෙකට සම්පූර්ණයෙන් වෙනස් ගණනය කිරීම් කළහැකි බවයි. මෙය දත්ත සමාන්තරකරණයෙන් වෙනස් වන්නේ ඒවායේ සිදුවන්නේ එකම දත්ත කට්ටලයේ එකම ගණනය කිරීම් සිදුවන බැවිනි. වැඩ සමාන්තරකරණය සාමාන්‍යයෙන් ප්‍රශ්නයේ විශාලත්වය සමග වැඩි නොවේ.

දෘඩාංග

මතකය සහ සන්නිවේදනය

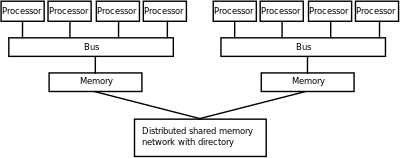
A logical view of a Non-Uniform Memory Access (NUMA) architecture. Processors in one directory can access that directory's memory with less latency than they can access memory in the other directory's memory.

සමාන්තර පරිගණක ප්‍රභේද (Classes of parallel computers)

සමාන්තර පරිගණක ඒවායේ දෘඩාංග සමාන්තරකරණය සදහා දක්වන සගයෝගය මත වර්ග කීපයකට වෙන්කළ හැක. මෙම වර්ගීකරණය සාමාන්‍ය පරිගණක වර්ගීකරනයටද සමීප සබඳතා දක්වයි. උදාහරණ ලෙස කොට්ඨාශ පරිගණනය සමාන්තර පරිගණනයේ මෙන්ම සමමිතික පරිගණනයේදීද දැකියහැක.

බහු හර පරිගණනය (Multicore computing)

බහු හර දත්ත සකසනයක් තුළ දත්ත සැකසුම් ඒකක එකකට වඩා වැඩි ගණනක් එකම චිපයේ අඩංගු කර තනා ඇත. බහු හර (core) දත්ත සකසනයකට එකවර විධාන කීපයක් නිකුත්කළහැක. එමෙන්ම සෑම බහු හර දත්ත සකසනයකටම super-scalar උපාංගයක් ලෙසද ක්‍රියා කළහැක. එනම් සෑම හරයකටම එකම විධාන ගලායාමකින්ම විධාන කට්ටල කීපයක් නිකුතකළ හැක. බහුනූල් පරිගණනය මෙම තාක්ශණයට කලින් පැවති ව්‍යාජ බහු හර තාක්ෂණයයි. Sony PlayStation 3 ක්‍රීඩා උපාංගය සදහා සකසන ලද IBM සමාගමේ Cell ක්‍ෂුද්‍ර සකසනය මෙසේ සකසනලද බහු හර සකසනයකි.

සමමිතික බහුසකසනය (Symmetric multiprocessing)

සමමිතික බහුසකසනයක් යනු එකම මතකයක් හවුලේ භාවිතයට ගන්නා එක සමාන දත්ත සකසන රාශියක එකතුවකි^[20]. මෙහි තාක්ශණික ශිල්පයට (bus architectures) අනුව දත්ත සලසන 32 කට වැඩි ගණනක් එකිනෙක සම්බන්ද කළනොහැක^[21]. මෙසේ විශාල දත්ත සැකසුම් ගණනක් යොදා නොගන්නා නිසාත් විශාල පරිගණක මගින් ලබාගන්නා කලාප පළල අඩු නිසාත් මේවා වියදම් කරන මුදලේ ප්‍රමාණය අනුව ඉතා කාර්යක්‍ෂම වේ.

ව්‍යාප්ත පරිගණනය (Distributed computing)

ව්‍යාප්ත පරිගණක (නොහොත් ව්‍යාප්ත මතක බහු දත්ත සකසන) යනු දත්ත සකසනයන් එකිනෙක ජාලගත කරනලද ව්‍යාප්ත මතක පරිගණක පද්දති වේ. මේවා විශාල භූගෝලීය ප්‍රදේශයක පතුරවාලිය හැකිය.

පොකුරු පරිගණනය (Cluster computing)

පරිගණක පොකුරක් යනු එකිනෙකට ලිහින්ව සම්බන්දිත එක්ව වැඩ කරන පරිගණක රාශියක එකතුවකි^[22]. පොකුරු පරිගණනයේදී ස්වාධීන පරිගණක කීපයක් එකිනෙක ජාලගත කර ඇති අතර ඒවාට යොදන භාරය නිසි ලෙස තුලනය කිරීමට (load balancing) නම් එම පරිගණක සමමිතික නොවියයුතුය. ප්‍රචලිතම පොකුරු පරිගණක වර්ගය Beowulf නම් පොකුරු පරිගණකයයි. වාණිජ පරිගණක කීපයක් (commercial off-the-shelf) TCP/IP Ethernet වර්ගයේ ප්‍රාදේශීය ජාලයකට (local area network) සම්බන්ද කිරීමෙන් මෙම ජාල තනා ඇත^[23]. මෙම තාක්ෂණය දියුණු කරන ලද්දේ Thomas Sterling සහ Donald Becker විසිනි. ලොව වේගවත්ම සුපිරි පරිගණක 500 (TOP500) අතරින් අති බහුතරය මෙසේ පොකුරු පරිගණක ලෙස සැකසූ සුපිරි පරිගණක වේ^[24].

විශාලිත සමාන්තර පරිගණනය (Massive parallel processing)

විශාලිත සමාන්තර දත්ත සකසනයක් යනු ජාලගත කරනලද දත්ත සකසන රාශියක් සහිත තනි පරිගණකයකි. පොකුරු පරිගණකවල ලක්ශණ රාශියක් මෙම පරිගණක විශේෂයේද දැකියහැක. එහෙත් පොකුරු පරිගණනයේදී මෙන් නොව විශාලිත සමාන්තර පරිගණකවල විශේෂිත වූ සම්බන්දක ජාල දැකියහැක. එමෙන්ම මේවා පොකුරු පරිගණන පද්දති වලට වඩා විශාල වේ. දත්ත සැකසුම් ඒකක 100 කට වඩා විශාල සංඛ්‍යාවක් ඇති අතර සෑම දත්ත සකසනයක් සදහාම මෙහෙයුම් පද්දතියක් සහ වැඩසටහන් වෙන වෙනම අඩංගු වේ^[25]. මේවායේ සෑම උප පද්දතියක්ම එකිනෙකට අධිවේගීව සම්බන්ද වී ඇත.^[26]

කොට්ටාශ පරිගණනය (Grid computing)

කොට්ටාශ පරිගණනය යනු සමාන්තර පරිගණනයේ වඩාත්ම පැතිරුන අවස්ථාවයි. මෙහිදී සිදුවන්නේ යම් දෙනලද ගැටලුවක් නිරාකරණය සදහා අන්තර්ජාලය ඔස්සේ පරිගණක රාශියක් ජාලගත වී සන්නිවේදනය කිරීමයි. එහෙත් අන්තර්ජාල පහසුකම් වල ඇති අඩු කලාප පළල නිසාත් අධික ගුප්තතාවය (latency) නිසාත් විශාල ප්‍රමාණයේ සමාන්තරික ප්‍රශ්න (embarrassingly parallel) සදහා පමණක් මෙම ක්‍රමය යොදාගනී. කොට්ටාශ පරිගණන වැඩසටහන් විශාල සංඛ්‍යාවක් අතරින් SETI@home සහ Folding@Home ව්‍යාපෘතීන් වඩාත් ප්‍රකට ඒවායි^[27].

බොහෝ කොට්ටාශ පරිගණන වැඩසටහන් මගින් යෙදුම් සහ පද්ධති මෘදුකාංග අතර අතරමැදියෙකු ලෙස ක්‍රියා කරන මෘදුකාංග (middleware) තම කටයුතු පහසු කරගැනීමට යොදාගනී. මේවා පරිගණක මෙහෙයුම් පද්දතිය සහ වැඩසටහන් අතර අතමැදියෙකු ලෙස ක්‍රියා කරමින් ජාලගත සම්පත් කළමනාකරණය සහ මෘදුකාංග අතුරුමුහුණත් ප්‍රමිතිගත කිරීම සිදුකරයි. කොට්ටාශ පරිගණනය සදහා යොදාගන්නා බහුලතම middleware වැඩසටහන Berkeley Open Infrastructure for Network Computing (BOINC) නම් වේ.

විශේෂිත සමාන්තර පරිගණනය (Specialized parallel computers)

සමාන්තර පරිගණන ක්ෂේත්‍රයේ යම් කොටසකට පමණක් විශේෂිත වූ සමාන්තර පරිගණන උපකරණද ඇත. ඒවා තමන්ට විශේෂිත වූ විෂය පථයක ගැටලු නිරාකරණය සදහා විශේෂිත වී ඇත.

Reconfigurable computing with field-programmable gate arrays

නැවත සැකසියහැකි පරිගණනය (Reconfigurable computing) යනු field-programmable gate array (FPGA) හි භාවිතයකි. FPGA මගින් යම් ඉලක්කගත කර්යයක් සඳහා තමන් විසින්ම යලි තම පරිපථ සකසා ගැනීම සිදුකරයි.

FPGA උපකරණ ක්‍රමලේඛනය කිරීම සදහා VHDL හෝ Verilog වැනි දෘඩාංග විස්තරකරණ (hardware description languages) භාෂා යොදාගනී. කෙසේ වෙතත් එම ක්‍රමලේඛන භාෂා වලින් ක්‍රමලේඛනය කිරීම ඉතා වෙහෙසකාරී වියහැක. මේ නිසා සමාගම් කීපයක් මගින් C සිට HDL යා කරන ක්‍රමලේඛන භාෂා කීපයක් සාදනලදී. C ක්‍රමලේඛන භාෂාව බොහෝ දෙනාට හුරුපුරුදු නිසා මෙම නව භාෂාව මගින් ක්‍රමලේඛනය කිරීම පසු විය. මෙසේ සාදන ලද භාෂා අතරින් ප්‍රචලිත භාෂා අතර Mitrion-C, Impulse C, DIME-C, සහ Handel-C ප්‍රමුඛවේ.

AMD සමාගම මගින් එහි HyperTransport තාක්ෂණය තෙවන පාර්ශව සදහා විවෘත කිරීමත් සමගම අධි කාර්යසාධක නැවත සකස් කළහැකි පරිගණනය තවත් දියුණුවක් ලැබීය.

ග්‍රැෆික දත්ත සකසන භාවිතයෙන් පොදු අරමුණු සදහා පරිගණනය (GPGPU)

General-purpose computing on graphics processing units (GPGPU)

ග්‍රැෆික දත්ත සකසන භාවිතයෙන් පොදු අරමුණු සදහා පරිගණනය යනු මෑතකාලීනව බෙහෙවින් ප්‍රකට වූ පරිගණක ඉන්ජිනේරු ගවේශණයකි. ග්‍රැෆික දත්ත සකසන විශේෂයෙන්ම සකසා ඇත්තේ ග්‍රැෆික දත්ත සකසනය සදහායි. දත්ත සමාන්තරව මෙහෙයවීමට, විශේෂයෙන්ම රේඛීය වීජ ගණිතයේ (linear algebra matrix)එන මෙහෙයුම් සඳහා ග්‍රැෆික දත්ත සකසන භාවිතවේ.

මුල්කාලීනව ග්‍රැෆික දත්ත සකසන භාවිතයෙන් පොදු අරමුණු සදහා පරිගණන වැඩසටහන් භාවිතා කළේ සාමාන්‍ය ග්‍රැෆික දත්ත සකසන භාවිත කරන වැඩසටහන් අතුරු මුහුණතයි. කෙසේ වෙතත් ග්‍රැෆික දත්ත සකසන වල භාවිතය සදහාම නව ක්‍රමලේඛන වැඩසටහන් සහ වේදිකා Nvidia (CUDA) සහ AMD (CTM) වැනි සමාගම් මගින් හදුන්වා දෙනලදී. අනෙක් ක්‍රමලේඛන භාෂා අතර BrookGPU, PeakStream සහ RapidMind ප්‍රමුඛ වේ. සාමාන්‍ය දත්ත සැකසුම් ඒකක සහ ග්‍රැෆික දත්ත සැකසුම් ඒකක සඳහා පොදු රාමුවක් (framework) consortium Khronos සමූහය මගින් OpenCL නමින් හදුන්වාදුන් අතර Apple, Intel, Nvidia සහ අනෙකුත් සමාගම් එම සම්මතයට අනුව තම නිෂ්පාදන සිදුකරයි.

වැඩසටහන් විශේෂිත සංඝත පරිපථ (Application-specific integrated circuits)

වැඩසටහන් විශේෂිත සංඝත පරිපථ කීපයක්ම සමාන්තර පරිගණනය සඳහා යෙදවීම් කර ඇත^[28]^[29]^[30].

ASIC (වැඩසටහන් විශේෂිත සංඝත පරිපථ - Application-specific integrated circuits) විශේෂයෙන්ම යම් වැඩසටහනක් සදහා සකසා ඇති නිසා ඒවා අදාල ක්‍රියාව සදහා උපරිම කාර්යක්‍ෂමතාවක් පෙන්වයි. කෙසේ වෙතත් ASIC සාදනු ලබන්නේ X කිරණ ලිතෝ මුද්‍රණය (X-ray lithography) මගින් වන අතර මෙය බෙහෙවින් මිල අධික තාක්ශණයකි^[31]. ASIC වල කාර්යක්ෂමතාවය වැඩි උවද පොදු අරමුණු සදහා පරිගණනය මූවර්ගේ නීතියට අනුව වේගයෙන් දියුණු වන නිසා මෙම කාර්යක්ශමතාවය එතරම් ඵලදායි නැත. අධික මූලික වියදමත් පොදු අරමුණු සදහා පරිගණනය මගින් ASIC අභිබවනය කරන නිසාත් මේවා බහුලව දැකියහැකි නොවුවද වර්තමානයේ පෙටා ෆ්ලොප්ස් මට්ටමේ සුපිරි පරිගණක වලද (RIKEN MDGRAPE-3) මෙම තාක්ශණය දැකියහැක.

දෛශීය දත්ත සකසන (Vector processors)

දෛශීය දත්ත සකසන යනු එකම විධානය විශාල දත්ත කට්ටලයක සම්පූර්ණ කළහැකි වර්ගයේ පරිගණක වර්ගයකි. උපුටා ගැනීම: "Vector processors have high-level operations that work on linear arrays of numbers or vectors. An example vector operation is A = B × C, where A, B, and C are each 64-element vectors of 64-bit floating point numbers."^[32] They are closely related to Flynn's SIMD classification.^[32]

Cray පරිගණක පද්දති තම දෛශීය දත්ත සකසන හැකියාව නිසා 1970 සහ 1980 දශක වලදී මහත් ජනප්‍රියත්වයක් ලද්දේය. එසේ වෙතත් අද මෙම දෛශීය දත්ත සකසන භාවිතයේ නොමැත. නූතන දත්ත සකසන විධාන පද්දති (processor instruction sets) වලද යම් තරමකින් දෛශීය දත්ත සකසන විධාන එක්කර ඇත. AltiVec සහ Streaming SIMD Extensions උදාහරණ වේ.

මෘදුකාංග

සමාන්තර පරිගණන භාෂා

සමාන්තර පරිගණනය සඳහා ‍සමගාමී ක්‍රමලේඛන භාෂා (Concurrent programming languages), පුස්තකාල (Library), වැඩසටහන් අතුරුමුහුණත් (Application programming interface (APIs)) සහ සමාන්තර ක්‍රමලේඛන ආකෘති (parallel programming models) තනා ඇත. මෙම ක්‍රමලේඛන භාෂා ඒවායේ දත්ත නිර්මාන ශිල්පය සදහා උපයෝගී කරගන්නා උපකල්පන පාදක කරගෙන විවිධ කොටස් වලට බෙදේ. ඒවා නම් හවුල් මතකය (shared memory), ව්‍යාප්ත මතකය (distributed memory) හෝ හවුල් ව්‍යාප්ත මතකයයි (shared distributed memory).

හවුල් මතක ක්‍රමලේඛන භාෂා එකිනෙක අතර සන්නිවේදනය කරනුයේ හවුල් දත්ත විචල්‍ය මගිනි. ව්‍යාප්ත මතකය මේ සදහා පණිවිඩ පරිවහන (message passing) ක්‍රමය අනුගමනය කරයි. POSIX නූල් (thread) සහ OpenMP යනු මේ සදහා බහුලව යොදාගන්නා මතක වැඩසටහන් ක්‍රමලේඛන අතුරුමුහුණත්ය. MPI (Message Passing Interface) යනු මෙසේ තොරතුරු ගෙනයාම සදහා යොදාගන්නා ප්‍රමුඛතම තොරතුරු පරිවහන ක්‍රමයයි^[33]. සමාන්තර පරිගණනය සදහා යොදාගන්නා තවත් සංකල්පයක් වන්නේ අනාගත ගිවිසුම් සංකල්පයයි (Futures and promises). මෙයින් කියවෙන්නේ යම් වැඩසටහනක් මගින් අනෙක් වැඩසටහන සදහා අවශ්‍ය දත්ත අනාගතයේදී සැපයීම සදහා පොරොන්දු වීමයි. OpenHMPP යනු දිශානුගත පරිගණක ක්‍රමලේඛන ආකෘතියකි. එමගින් කාර්යක්ෂම දෘඩාංග ත්වරණයක් සදහා කාරක රීති (syntax) සැපයීමත්, දෘඩාංග වල සිට දත්ත එහා මෙහා ගෙනයාම දියුණු කිරීමත් සිදුකරයි.

ස්වයංක්‍රීය සමාන්තරකරණය

අනුක්‍රමික වැඩසටහනක් සංග්‍රාහකයක් (compiler) මගින් ස්වයංක්‍රීයව සමාන්තරකරණය කළහැකි නම් එය සමාන්තර පරිගණනයේදී ඉතා වැදගත් වේ. ස්වයංක්‍රීය සමාන්තරකරණය සදහා දශක ගණනාවක සිට පර්යේශණ කළද එය තවමත් සාර්ථක මට්ටමක නොපවතී^[34].

සාමාන්‍ය භාවිතයේ ඇති සමාන්තරකරණය සදහා වූ ක්‍රමලේඛන භාෂා සම්පූර්ණ ලෙස සමාන්තර භාවයෙන් හෝ අර්ධ සමාන්තර භාවයෙන් යුතුවේ. මේවායේ සංග්‍රාහක වෙත විධාන නිකුත් කිරීම මගින් සමාන්තරගතකරණක කරගතයුතුය. කෙසේ වෙතත් සම්පූර්ණයෙන්ම සමාන්තරගත පරිගණක ක්‍රමලේඛන භාෂා ඇත්තේ කීපයක් පමණි. ඒවා නම් SISAL, Parallel Haskell සහ ( FPGAs සදහා) Mitrion-C.

වැඩසටහන් සමීක්ශණය (Application check-pointing)

පරිගණකයක් විශාල සහ සංකීරණ වන තරමට එහි බිදවැටුමක් හෝ වැරැද්දක් වීමේ සම්භාවිතාවයද වැඩි වේ. වැඩසටහන් සමීක්ශණය යනු පරිගණක පද්දතියක් මගින් දැනට පවතින විචල්‍යයන් සහ සම්පත් වෙන්කරගෙන ඇති ආකාරය පිළිබඳව තබාගන්න සටහනයි. කුමන ආකාරයක හෝ වැටසටහන් බිදවැටුමකදී මෙම දත්ත භාවිතයෙන් නැවත වැඩසටහන පණගැන්වීම කළහැක. මේ නිසා හදිසි බිඳවැටුමකදී වැඩසටහන නැවත මූලික ස්ථානයේ සිට පණගැන්වීමකින් තොරව අවසාන වැඩසටහන් සමීක්ශණ ස්ථානයේ සිට එය ක්‍රියාකාරී කිරීම කළහැක. දින ගණන්, මාස ගණනින් ක්‍රියාකාරී වන වැඩසටහන් සදහා මෙය ඉතා වැදගත් වේ.

Algorithmic ක්‍රමය

සමාන්තර පරිගණක විශාල සහ ප්‍රභල වීමත් සමගම අතීතයේ විසදීමට අසීරු වූ විවිධ ගැටලුද විසදීමේ හැකියාව ඒවාට ලැබිනි. වර්තමානයේ සමාන්තර පරිගණනය ඉතා විශාල පරාසයක භාවිතයන් සදහා යොදාගනී. bioinformatics, protein folding සහ sequence analysis පමණක් නොව ආර්ථික කටයුතු mathematical finance සදහාද මේවා යොදාගනී. සමාන්තර පරිගණනයේදී පැන නගින පොදු ගැටලු කිහිපයක් පහත දැක්වේ.^[35]

Dense linear algebra
Sparse linear algebra
Spectral methods (උදාහරණ Cooley–Tukey FFT algorithm|Cooley–Tukey fast Fourier transform)
n-body simulation|n-body problems (උදාහරණ Barnes–Hut simulation)
Regular grid|Structured grid problems (උදාහරණ Lattice Boltzmann methods)
Unstructured grid problems (උදාහරණ finite element analysis)
Monte Carlo method|Monte Carlo simulation
Combinational logic (උදාහරණ Brute force attack|brute-force cryptographic techniques)
Graph traversal (උදාහරණ sorting algorithms)
Dynamic programming
Branch and bound methods
Graphical models (උදාහරණ hidden Markov models and constructing Bayesian networks)
Finite-state machine simulation

ඉතිහාසය

සමාන්තරකරණයේ සැබෑ මූලය ෆෙඩ්රිකෝ ලූගි, කොන්ට් මෙනබ්‍රා (Federico Luigi, Conte Menabrea) සහ චර්ස් බැබේජ්ගේ (Charles Babbage) විග්‍රහාත්මක එන්ජිමෙහි කටු සටහන (Analytic Engine) දක්වා අතීතයට දිවයයි.^[37]^[38] IBM සමාගම මගින් 1974 දී හදුන්වා දුන් 704 නම් පරිගණකය ප්‍රථමවරට සම්පූර්ණයෙන් ස්වයංක්‍රීය ඉපිලෙන ලක්ෂ ගණිතාංක (floating point) විධාන භාවිතයට ගත් පරිගණකයයි^[39].

1958 දී S. ගිල් (S. Gill Ferranti) විසින් සමාන්තර පරිගණනයේදී ශාකනය සහ පොරොත්තුව පිළිබඳව සකච්චා කරන ලදී^[40]. එමෙන්ම 1958දී IBM සමාගමේ පර්යේෂකයන් වූ ජෝන් කෝක් (John Cocke) සහ ඩැනියෙල් ස්ලොට්නික් (Daniel Slotnick) යන අය විසින් අංක ගණිතය සදහා සමාන්තර පරිගණනය යොදා ගැනීම සාකච්චා කරන ලදී^[41]. Burroughs සමාගම (Burroughs Corporation) මගින් 1962 දී D825 නම් පරිගණකය හදුන්වා දෙනලදී. මෙය දත්ත සැකසුම් ඒකක හතරක් සහිත මතක මොඩියුල 16 කට හරස් දඩු ස්වීචයක් (crossbar switch) ඔස්සේ ඇතුල්වියහැකි පරිදි නිපදවන ලදී^[42]. 1967 දී අම්ඩාල් සල ස්ලොට්නික් විසින් AFIPS (American Federation of Information Processing Societies) සම්මන්ත්‍රණය සදහා සමාන්තර පරිගණනය සදහා සාධ්‍යතාවය පිළිබඳව විවාදයක් ප්‍රකාශයට පත්කරන ලදී.

1969 දී අමෙරිකාවේදී හනිවෙල් සමාගම (Honeywell) මගින් ප්‍රථම Multics පද්දතිය හදුන්වා දෙනලදී. එය සමමිතික බහු දත්ත සකසන ඒකකයක් වූ අතර දත්ත සකසන අටක් එකවර සමාන්තරව ක්‍රියාකරවීමේ හැකියාව තිබිනි. 1970 දී කානෙජි මෙලෝන් විශ්ව විද්‍යාලයේ (Carnegie Mellon University) ඇරබි C.mmp නම් දත්ත සකසන එකකට වඩා ඇති බහු දත්ත සකසන පිළිබඳ ව්‍යාපෘතිය එවැනි වර්ගයේ ප්‍රථම පද්දති වලින් එකක් විය.

SIMD සමාන්තර පරිගණන යන්ත්‍ර 1970 දශකය දක්වා අතීතයකට විහිදේ. මුල් කාලීනව ඉදිකෙරුනු SIMD පද්දති සදහා පෙළබවීමක් ලැබුනේ බහු විධාන සහිත දත්ත සැකසුම් ඒකක මෙහෙයුම් පද්දති (control unit) වල ගේට්ටු ප්‍රමාදය (gate delay) හේතුවෙනි. මේ අතර ස්ලොට්නික් විසින් විශාල ප්‍රමාණයේ සමාන්තර පරිගණන ඒකකයක් තැනීම ඇරබීය. ඒ Lawrence Livermore ජාතික විද්‍යාගාරය ([Lawrence Livermore National Laboratory) සදහායි. ඔහුගේ අරමුණ සදහා මූල්‍ය සම්පාදනය අමෙරිකානු ගුවන් හමුදාව මගින් දරනු ලැබීය. එහි ප්‍රථිපල ලෙස ILLIAC IV පරිගණකය නිර්මානය විය. එහෙත් මෙම ව්‍යාපෘතිය එතරම් සාර්ථක නොවුන අතර ඇස්තමේන්තුගත කාලයට වඩා වැඩි කාලයක් සහ සිවු ගුණයක් මුදල් වැය කර 1976 වනවිට අවසන් කළ මෙම පරිගණකයට වඩා එකල ජනප්‍රියව තිබූ Cray-1 වැනි සුපිරි පරිගණක වේගවත් විය.^[43].

මේවත් බලන්න

මූලාශ්‍ර

^ Almasi, G.S. and A. Gottlieb (1989). Highly Parallel Computing. Benjamin-Cummings publishers, Redwood City, CA.
^ S.V. Adve et al. (November 2008). "Parallel Computing Research at Illinois: The UPCRC Agenda" (PDF). Parallel@Illinois, University of Illinois at Urbana-Champaign. "The main techniques for these performance benefits – increased clock frequency and smarter but increasingly complex architectures – are now hitting the so-called power wall. The computer industry has accepted that future performance increases must largely come from increasing the number of processors (or cores) on a die, rather than making a single core go faster."
^ Asanovic et al. Old [conventional wisdom]: Power is free, but transistors are expensive. New [conventional wisdom] is [that] power is expensive, but transistors are "free".
^ Asanovic, Krste et al. (December 18, 2006). "The Landscape of Parallel Computing Research: A View from Berkeley" (PDF). University of California, Berkeley. Technical Report No. UCB/EECS-2006-183. "Old [conventional wisdom]: Increasing clock frequency is the primary method of improving processor performance. New [conventional wisdom]: Increasing parallelism is the primary method of improving processor performance ... Even representatives from Intel, a company generally associated with the 'higher clock-speed is better' position, warned that traditional approaches to maximizing performance through maximizing clock speed have been pushed to their limit."
^ Patterson, David A. and John L. Hennessy (1998). Computer Organization and Design, Second Edition, Morgan Kaufmann Publishers, p. 715. ISBN 1-55860-428-6.Patterson, David A. and John L. Hennessy (1998). Computer Organization and Design, Second Edition, Morgan Kaufmann Publishers, p. 715. ISBN 1-55860-428-6
^ a b Barney, Blaise. "Introduction to Parallel Computing". Lawrence Livermore National Laboratory. Retrieved 2007-11-09.
^ ^ Hennessy, John L. and David A. Patterson (2002). Computer Architecture: A Quantitative Approach. 3rd edition, Morgan Kaufmann, p. 43. ISBN 1-55860-724-2.
^ Rabaey, J. M. (1996). Digital Integrated Circuits. Prentice Hall, p. 235. ISBN 0-13-178609-1.
^ Flynn, Laurie J. "Intel Halts Development of 2 New Microprocessors". The New York Times, May 8, 2004. Retrieved on April 22, 2008.
^ Flynn, Laurie J. "Intel Halts Development of 2 New Microprocessors". The New York Times, May 8, 2004. Retrieved on April 22, 2008.Moore, Gordon E. (1965). "Cramming more components onto integrated circuits" (PDF). Electronics Magazine. pp. 4. Retrieved 2006-11-11.
^ Amdahl, G. (April 1967) "The validity of the single processor approach to achieving large-scale computing capabilities". In Proceedings of AFIPS Spring Joint Computer Conference, Atlantic City, N.J., AFIPS Press, pp. 483–85.
^ Reevaluating Amdahl's Law (1988). Communications of the ACM 31(5), pp. 532–33.
^ Bernstein, A. J. (October 1966). "Program Analysis for Parallel Processing,' IEEE Trans. on Electronic Computers". EC-15, pp. 757–62.
^ Lamport, Leslie (September 1979). "How to Make a Multiprocessor Computer That Correctly Executes Multiprocess Programs", IEEE Transactions on Computers, C-28,9, pp. 690–91.
^ Culler, David E.; Jaswinder Pal Singh and Anoop Gupta (1999). Parallel Computer Architecture - A Hardware/Software Approach. Morgan Kaufmann Publishers, p. 15. ISBN 1-55860-343-3.
^ Culler et al. p. 15.
^ Patt, Yale (April 2004). "The Microprocessor Ten Years From Now: What Are The Challenges, How Do We Meet Them? (wmv). Distinguished Lecturer talk at Carnegie Mellon University. Retrieved on November 7, 2007.
^ Culler et al. p. 124.
^ Culler et al. p. 125.
^ Hennessy and Patterson, p. 549.
^ Patterson and Hennessy, p. 714.
^ What is clustering? Webopedia computer dictionary. Retrieved on November 7, 2007.
^ Beowulf definition. සංරක්ෂණය කළ පිටපත 2012-10-10 at the Wayback Machine PC Magazine. Retrieved on November 7, 2007.
^ Architecture share for 06/2007 සංරක්ෂණය කළ පිටපත 2007-11-14 at the Wayback Machine. TOP500 Supercomputing Sites. Clusters make up 74.60% of the machines on the list. Retrieved on November 7, 2007.
^ Hennessy and Patterson, p. 537.
^ MPP Definition. සංරක්ෂණය කළ පිටපත 2013-05-11 at the Wayback Machine PC Magazine. Retrieved on November 7, 2007.
^ Kirkpatrick, Scott (January 31, 2003). "Computer Science: Rough Times Ahead". Science, Vol. 299. No. 5607, pp. 668 - 669. DOI: 10.1126/science.1081623
^ Maslennikov, Oleg (2002). "Systematic Generation of Executing Programs for Processor Elements in Parallel ASIC or FPGA-Based Systems and Their Transformation into VHDL-Descriptions of Processor Element Control Units". සංරක්ෂණය කළ පිටපත 2020-02-11 at the Wayback Machine Lecture Notes in Computer Science, 2328/2002: p. 272.
^ Shimokawa, Y.; Y. Fuwa and N. Aramaki (18–21 November 1991). A parallel ASIC VLSI neurocomputer for a large number of neurons and billion connections per second speed. IEEE International Joint Conference on Neural Networks. 3: pp. 2162–67.
^ Acken, K.P.; M.J. Irwin, R.M. Owens (July 1998). "A Parallel ASIC Architecture for Efficient Fractal Image Coding". The Journal of VLSI Signal Processing, 19(2):97–113(17)
^ Kahng, Andrew B. (June 21, 2004) "Scoping the Problem of DFM in the Semiconductor Industry." University of California, San Diego. "Future design for manufacturing (DFM) technology must reduce design [non-recoverable expenditure] cost and directly address manufacturing [non-recoverable expenditures] – the cost of a mask set and probe card – which is well over $1 million at the 90 nm technology node and creates a significant damper on semiconductor-based innovation."
^ ^a ^b Patterson and Hennessy, p. 751.
^ The Sidney Fernbach Award given to MPI inventor Bill Gropp refers to MPI as "the dominant HPC communications interface"
^ Shen, John Paul and Mikko H. Lipasti (2005). Modern Processor Design: Fundamentals of Superscalar Processors. McGraw-Hill Professional. p. 561. ISBN 0-07-057064-7. "However, the holy grail of such research - automated parallelization of serial programs - has yet to materialize. While automated parallelization of certain classes of algorithms has been demonstrated, such success has largely been limited to scientific and numeric applications with predictable flow control (e.g., nested loop structures with statically determined iteration counts) and statically analyzable memory access patterns. (e.g., walks over large multidimensional arrays of float-point data)."
^ Asanovic, Krste, et al. (December 18, 2006). The Landscape of Parallel Computing Research: A View from Berkeley (PDF). University of California, Berkeley. Technical Report No. UCB/EECS-2006-183. See table on pages 17–19.
^ Patterson and Hennessy, pp. 749–50: "Although successful in pushing several technologies useful in later projects, the ILLIAC IV failed as a computer. Costs escalated from the $8 million estimated in 1966 to $31 million by 1972, despite the construction of only a quarter of the planned machine ... It was perhaps the most infamous of supercomputers. The project started in 1965 and ran its first real application in 1976."
^ Menabrea, L. F. (1842). Sketch of the Analytic Engine Invented by Charles Babbage. Bibliothèque Universelle de Genève. Retrieved on November 7, 2007.
^ Patterson and Hennessy, p. 753.
^ da Cruz, Frank (2003). "Columbia University Computing History: The IBM 704". Columbia University. සම්ප්‍රවේශය 2008-01-08.
^ Parallel Programming, S. Gill, The Computer Journal Vol. 1 #1, pp2-10, British Computer Society, April 1958.
^ Wilson, Gregory V (1994). "The History of the Development of Parallel Computing". Virginia Tech/Norfolk State University, Interactive Learning with a Digital Library in Computer Science. සම්ප්‍රවේශය 2008-01-08.
^ Anthes, Gry (November 19, 2001). "The Power of Parallelism". Computerworld. සම්ප්‍රවේශය 2008-01-08.
^ Patterson and Hennessy, pp. 749–50: "Although successful in pushing several technologies useful in later projects, the ILLIAC IV failed as a computer. Costs escalated from the $8 million estimated in 1966 to $31 million by 1972, despite the construction of only a quarter of the planned machine ... It was perhaps the most infamous of supercomputers. The project started in 1965 and ran its first real application in 1976."

භාහිර පුරුක්

[1] Almasi, G.S. and A. Gottlieb (1989). Highly Parallel Computing. Benjamin-Cummings publishers, Redwood City, CA.

[2] S.V. Adve et al. (November 2008). "Parallel Computing Research at Illinois: The UPCRC Agenda" (PDF). Parallel@Illinois, University of Illinois at Urbana-Champaign. "The main techniques for these performance benefits – increased clock frequency and smarter but increasingly complex architectures – are now hitting the so-called power wall. The computer industry has accepted that future performance increases must largely come from increasing the number of processors (or cores) on a die, rather than making a single core go faster."

[3] Asanovic et al. Old [conventional wisdom]: Power is free, but transistors are expensive. New [conventional wisdom] is [that] power is expensive, but transistors are "free".

[4] Asanovic, Krste et al. (December 18, 2006). "The Landscape of Parallel Computing Research: A View from Berkeley" (PDF). University of California, Berkeley. Technical Report No. UCB/EECS-2006-183. "Old [conventional wisdom]: Increasing clock frequency is the primary method of improving processor performance. New [conventional wisdom]: Increasing parallelism is the primary method of improving processor performance ... Even representatives from Intel, a company generally associated with the 'higher clock-speed is better' position, warned that traditional approaches to maximizing performance through maximizing clock speed have been pushed to their limit."

[5] Patterson, David A. and John L. Hennessy (1998). Computer Organization and Design, Second Edition, Morgan Kaufmann Publishers, p. 715. ISBN 1-55860-428-6.Patterson, David A. and John L. Hennessy (1998). Computer Organization and Design, Second Edition, Morgan Kaufmann Publishers, p. 715. ISBN 1-55860-428-6

[6] Barney, Blaise. "Introduction to Parallel Computing". Lawrence Livermore National Laboratory. Retrieved 2007-11-09.

[7] Hennessy, John L. and David A. Patterson (2002). Computer Architecture: A Quantitative Approach. 3rd edition, Morgan Kaufmann, p. 43. ISBN 1-55860-724-2.

[8] Rabaey, J. M. (1996). Digital Integrated Circuits. Prentice Hall, p. 235. ISBN 0-13-178609-1.

[9] Flynn, Laurie J. "Intel Halts Development of 2 New Microprocessors". The New York Times, May 8, 2004. Retrieved on April 22, 2008.

[10] Flynn, Laurie J. "Intel Halts Development of 2 New Microprocessors". The New York Times, May 8, 2004. Retrieved on April 22, 2008.Moore, Gordon E. (1965). "Cramming more components onto integrated circuits" (PDF). Electronics Magazine. pp. 4. Retrieved 2006-11-11.

[11] Amdahl, G. (April 1967) "The validity of the single processor approach to achieving large-scale computing capabilities". In Proceedings of AFIPS Spring Joint Computer Conference, Atlantic City, N.J., AFIPS Press, pp. 483–85.

[12] Reevaluating Amdahl's Law (1988). Communications of the ACM 31(5), pp. 532–33.

[13] Bernstein, A. J. (October 1966). "Program Analysis for Parallel Processing,' IEEE Trans. on Electronic Computers". EC-15, pp. 757–62.

[14] Lamport, Leslie (September 1979). "How to Make a Multiprocessor Computer That Correctly Executes Multiprocess Programs", IEEE Transactions on Computers, C-28,9, pp. 690–91.

[15] Culler, David E.; Jaswinder Pal Singh and Anoop Gupta (1999). Parallel Computer Architecture - A Hardware/Software Approach. Morgan Kaufmann Publishers, p. 15. ISBN 1-55860-343-3.

[16] Culler et al. p. 15.

[17] Patt, Yale (April 2004). "The Microprocessor Ten Years From Now: What Are The Challenges, How Do We Meet Them? (wmv). Distinguished Lecturer talk at Carnegie Mellon University. Retrieved on November 7, 2007.

[Culler124-18] Culler et al. p. 124.

[Culler125-19] Culler et al. p. 125.

[HP549-20] Hennessy and Patterson, p. 549.

[21] Patterson and Hennessy, p. 714.

[22] What is clustering? Webopedia computer dictionary. Retrieved on November 7, 2007.

[23] Beowulf definition. සංරක්ෂණය කළ පිටපත 2012-10-10 at the Wayback Machine PC Magazine. Retrieved on November 7, 2007.

[24] Architecture share for 06/2007 සංරක්ෂණය කළ පිටපත 2007-11-14 at the Wayback Machine. TOP500 Supercomputing Sites. Clusters make up 74.60% of the machines on the list. Retrieved on November 7, 2007.

[25] Hennessy and Patterson, p. 537.

[26] MPP Definition. සංරක්ෂණය කළ පිටපත 2013-05-11 at the Wayback Machine PC Magazine. Retrieved on November 7, 2007.

[27] Kirkpatrick, Scott (January 31, 2003). "Computer Science: Rough Times Ahead". Science, Vol. 299. No. 5607, pp. 668 - 669. DOI: 10.1126/science.1081623

[28] Maslennikov, Oleg (2002). "Systematic Generation of Executing Programs for Processor Elements in Parallel ASIC or FPGA-Based Systems and Their Transformation into VHDL-Descriptions of Processor Element Control Units". සංරක්ෂණය කළ පිටපත 2020-02-11 at the Wayback Machine Lecture Notes in Computer Science, 2328/2002: p. 272.

[29] Shimokawa, Y.; Y. Fuwa and N. Aramaki (18–21 November 1991). A parallel ASIC VLSI neurocomputer for a large number of neurons and billion connections per second speed. IEEE International Joint Conference on Neural Networks. 3: pp. 2162–67.

[30] Acken, K.P.; M.J. Irwin, R.M. Owens (July 1998). "A Parallel ASIC Architecture for Efficient Fractal Image Coding". The Journal of VLSI Signal Processing, 19(2):97–113(17)

[31] Kahng, Andrew B. (June 21, 2004) "Scoping the Problem of DFM in the Semiconductor Industry." University of California, San Diego. "Future design for manufacturing (DFM) technology must reduce design [non-recoverable expenditure] cost and directly address manufacturing [non-recoverable expenditures] – the cost of a mask set and probe card – which is well over $1 million at the 90 nm technology node and creates a significant damper on semiconductor-based innovation."

[PH751-32] Patterson and Hennessy, p. 751.

[33] The Sidney Fernbach Award given to MPI inventor Bill Gropp refers to MPI as "the dominant HPC communications interface"

[34] Shen, John Paul and Mikko H. Lipasti (2005). Modern Processor Design: Fundamentals of Superscalar Processors. McGraw-Hill Professional. p. 561. ISBN 0-07-057064-7. "However, the holy grail of such research - automated parallelization of serial programs - has yet to materialize. While automated parallelization of certain classes of algorithms has been demonstrated, such success has largely been limited to scientific and numeric applications with predictable flow control (e.g., nested loop structures with statically determined iteration counts) and statically analyzable memory access patterns. (e.g., walks over large multidimensional arrays of float-point data)."

[35] Asanovic, Krste, et al. (December 18, 2006). The Landscape of Parallel Computing Research: A View from Berkeley (PDF). University of California, Berkeley. Technical Report No. UCB/EECS-2006-183. See table on pages 17–19.

[36] Patterson and Hennessy, pp. 749–50: "Although successful in pushing several technologies useful in later projects, the ILLIAC IV failed as a computer. Costs escalated from the $8 million estimated in 1966 to $31 million by 1972, despite the construction of only a quarter of the planned machine ... It was perhaps the most infamous of supercomputers. The project started in 1965 and ran its first real application in 1976."

[37] Menabrea, L. F. (1842). Sketch of the Analytic Engine Invented by Charles Babbage. Bibliothèque Universelle de Genève. Retrieved on November 7, 2007.

[PH753-38] Patterson and Hennessy, p. 753.

[39] Cruz, Frank (2003). "Columbia University Computing History: The IBM 704". Columbia University. සම්ප්‍රවේශය 2008-01-08.

[40] Parallel Programming, S. Gill, The Computer Journal Vol. 1 #1, pp2-10, British Computer Society, April 1958.

[G_Wilson-41] Wilson, Gregory V (1994). "The History of the Development of Parallel Computing". Virginia Tech/Norfolk State University, Interactive Learning with a Digital Library in Computer Science. සම්ප්‍රවේශය 2008-01-08.

[42] Anthes, Gry (November 19, 2001). "The Power of Parallelism". Computerworld. සම්ප්‍රවේශය 2008-01-08.

[infamous-43] Patterson and Hennessy, pp. 749–50: "Although successful in pushing several technologies useful in later projects, the ILLIAC IV failed as a computer. Costs escalated from the $8 million estimated in 1966 to $31 million by 1972, despite the construction of only a quarter of the planned machine ... It was perhaps the most infamous of supercomputers. The project started in 1965 and ran its first real application in 1976."

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]