සීසර් කේතාංකය
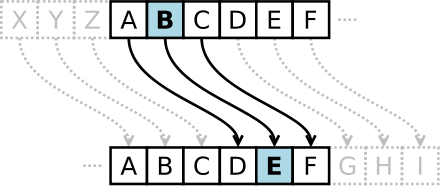
ගුප්ත කේතකරණයේ (cryptography) එන ඉතාම ප්රසිද්ධ හා පහසුම ක්රමයක් ලෙස සීසර් කේතාංකය හෙවත් සීසර්ගේ කේතාංකය හැඳින්විය හැක . මෙහිදි හුදු පෙළෙ ඇති සෑම අකුරක්ම නියත අකුරු ගණනකට පසුව හෝඩියෙ ඇති වෙනත් අකුරකින් ප්රතිස්ථාපනය කරනු ලැබේ. උදාහරණයක් ලෙස, ප්රතිස්ථාපනය ඉදිරියේ ඇති තුන්වන අකුර මගින් නම් සිදුවන්නේ A අකුර Dමගින් ද B අකුර E මගින් ද ප්රතිස්ථාපනය වේ. ජුලියස් සීසර්, ඔහුගේ සේනාධිපතිවරු සමඟ සන්නිවේදනය කිරීම සඳහා මෙම ක්රමය යොදා ගෙන ඇති නිසා එම නමින් හඳුන්වනු ලැබේ.
සීසර්-කේතාංකයේ භාවිතා වන ක්රමය ඉතාම පහසුවෙන් බිඳ දැමිය හැකි නිසා, වර්තමානයේ මෙමගින් ලබාදෙන සන්නිවේදන සුරක්ෂිත බාවය ඉතා අල්පය. නමුත් මෙහි ඇති පියවර විජනර-කේතාංකය වැනි වෙනත් සංකීර්ණ ක්රමවල අන්තර්ගතකර ඇත. වර්තමානයේ ROT13 පද්ධතියේ ඇතුලත් කර තිබේ.
උදාහරණ
[සංස්කරණය]අක්ෂර මාලාවන් දෙකක් පෙළට ගන්නවා අකුරු පරිවර්තනය වන ආකාරය පැහැදිලි කිරිය හැක. සාමාන්ය අක්ෂර මාලාව නියමිත ස්ථාන ගණනකින් වම් හෝ දකුණු පසට ඇති අකුරක් ප්රතිස්ථාපනය කිරීමෙන් කේතාංක අක්ෂර මාලාව සාදා ගත හැක.
සරල පාඨය: ABCDEFGHIJKLMNOPQRSTUVWXYZ
කේතනය: DEFGHIJKLMNOPQRSTUVWXYZABC
සාමාන්ය අකුරු පෙළේ ඇති සෑම අකුරක්ම අදාළ අක්ෂරය මගින් ප්රතිස්ථාපනය කිරීමෙන් කේතාංක පෙළ සෑදිය හැක. කේතාංකය කියවා තේරුම් ගැනීම මෙහි විරුද්ධ ක්රියාවයි.
කේතාංක අක්ෂර පෙළ: WKH TXLFN EURZQ IRA MXPSV RYHU WKH ODCB GRJ
සරල අක්ෂර පෙළ: the quick brown fox jumps over the lazy dog
මාපාංක ගණිතය භාවිතයෙන් ද කේතාංකනය කිරිය හැක. පළමුව අක්ෂර, ඉලක්කම් මගින් ප්රතිස්ථාපනය වේ (A = 0, B = 1, ..., Z = 25). [1] x අක්ෂරය n මගින් ප්රතිස්ථාපනය වී කේතාංකනය වන අයුරු පහත පෙන්වා ඇත. [2]
ප්රතිකේතනය වන අයුරු,
(ඉහත පිළිතුර 0...25 යන පරාසය තුළ පිහිටයි. x+n හෝ x-n එම පරාසයේ නොපවතී නම් එයට 26 ක් එකතු හෝ අඩු කිරිය යුතුයි. මෙම මාපාංකය සෙවීම සඳහා විවිධ අර්ථ දැක්වීම් ඇත.)
ඉහත දැක්වූ ප්රතිස්ථාපන ක්රමය සම්පූර්ණ පණිවුඩය පුරාම එලෙසම පවතී. එම නිසා සීසර් කේතාංකනය ඒකීය අක්ෂර මාලා ආදේෂනය ලෙස හඳුන්වයි. බහු අක්ෂර මාලා ආදේෂනය මෙහි විරුද්ධ ක්රියාපටිපාටිය වේ.
ඉතිහාසය සහ භාවිතය
[සංස්කරණය]
සීසර් කේතාංකය යන නාමය ලැබී ඇත්තේ ජුලියස් සීසර්ට ගෞරවයක් වශයෙනි. ඔහු විසින් මෙය ප්රතිස්ථාපනය ස්ථාන තුනක් මගින් සිදුකර යුධ හමුදා බට පිරිස් වලට පණිවුඩ යැවීම සඳහා භාවිතා කරන ලදි. ප්රථම වාර්තාගත කේතාංක ක්රමය මෙය වූවත් මීට පෙර ද වෙනත් ආදේශන කේතාංක ක්රම භාවිතා කර ඇත.
ඔහුගේ බෑනා ඕගස්ටස්ද මෙම ක්රමය දකුණු පැත්තට එක් ප්රතිස්ථාපනයක් යොදගෙන භාවිතා කර ඇත (අක්ෂර මාලාවේ ආරම්භයට නොපැමිණේ ). කේතාංකනය කිරීමේදී A වෙනුවට B, B වෙනුවට C ලෙසටද X වෙනුවට AA ද යොදා ගැනේ.
එම දිනවල සීසර් කේතාංකය කොතරම් දුරට බලවත්ව තිබුනාදැයි පැවසීමට අපහසු වූවත් සීසර්ගේ බොහෝ එදිරිකාරයන් අකුරු නොදත් අය නිසත්, සමහරුන් එම පණිවුඩය වෙනත් නුපුරුදු බසකින් ලියා ඇති බවට අනුමාන කළ නිසත් සෑහෙන දුරට සුරක්ෂිතව තිබූ බවට සිතිය හැක. කිසිම වාර්තාවක මෙම සරල ප්රතිස්ථාපන කේතාංකන ක්රමයට විසඳුමක් සඳහන් නොවේ. දැනට හමු වී ඇති පුරාණතම වාර්තාව වන්නේ නව වන සිවසේ අල්-කින්ඩි නම් අරාබි ජාතිකකු විසින් සංඛ්යාත විශ්ලේෂණය සොයා ගැනීමේදී ඉදිරිපත් කර වාර්තාවයි.[3]
මෙසූසාහි පිටුපස, දේවතාවන්ගේ නම් කේතාංකනය කිරීම සඳහා එක් ප්රතිස්ථාපනයක් සහිත සීසර් කේතාංකය භාවිතා කර ඇත. ජූස් පුද්ගලයින්ට මෙසූසා තබා ගැනීමට අවසර නොතිබූ කාලයේ සිට පැවත ආ දෙයක් ලෙසට මෙය සැලකිය හැක.
19 වන සියවසේ සරල කේතාංක ක්රම ආශ්රයෙන් පණිවුඩ හුවමාරු කිරීම සඳහා පුවත්පත් වල පුද්ගලික දැන්වීම් කොටස යොදා ගෙන ඇත. කාන් (1967) ද ටයිම්ස් [4] සඟරාවේ පෙම්වතුන් සන්නිවේදනය කරනවිට මෙම කේතාංක ක්රමය යොදාගන්නා බවට නිදර්ශන දක්වා ඇත. 1915 කාල වකවානුවේදී රුසියානු යුධබටයින්ට පුහුණු කිරීමට අපහසු ඉතා සංකීර්ණ කේතාංක ක්රම සඳහා විකල්පයක් ලෙසට යොදා ගෙන තිබේ. ජර්මානු හා ඔස්ට්රේලියානු වන්ට මෙය කියවා තේරුම් ගැනීම අසීරු කටයුත්තක් විය.[5]
වර්තමානයේ කුඩා ළමුන්ගේ කෙළිබඩු වල රහස් විකේතන වළලුවල සීසර් කේතාංකය දැක ගැනීමට පුළුවන. ROT13 ඇල්ගොරිදමේ ( වචන කියවා තේරුම් ගැනීමට නොහැකිවන ආකාරයට පත් කිරීම. බොහෝ විට Usenet වල භාවිතා වේ. බරපතළ ලෙස කේතාංක ක්රමයක් මෙන් යොදා නොගනී. ) ප්රතිස්ථාපන 13කින් සිදුවන සීසර් කේතාංකය යොදාගෙන තිබේ.[6]
සීසර් ක්රමයම විවිධ අකුරු සඳහා විවිධ ප්රතිස්ථාපන අගයන් යෙදූ විට විජනර කේතාංකය ලෙස හඳුන්වයි. එම අගය පුනරාවර්තන මූලික පදය මගින් සොයා ගනී. අහඹු ලෙස තෝරා ගන්නා එම වචනය නැවත භාවිතයට නොගැනේ. එමෙන්ම එය මුල් පණිවුඩය තරම්ම විශාල එකක් වූ විට කිසිවෙකුට සොයා ගැනීමට ද බිඳ දැමීමට ද නොහැකි වේ. ප්රායෝගිකව අවශ්ය කොන්දේසි සම්පූර්ණ කිරීමට නොහැකි තරම් අපහසුය. පණිවුඩයට වඩා කුඩා මූලික පදයක් ගත් විට එහි චක්රීය රටාව දියුණු සංඛ්යාත විශ්ලේෂණය මගින් සොයා ගත හැකි වේ.[7]
2006 අප්රේල් මාසයේ මාෆියා නායක ' බර්නාඩෝ ප්රොවෙන්සානො ' අල්ලා ගැනීමට හැකි වූයේ ඔහුගේ සීසර් කේතාංකය මගින් ලියා තිබූ පණිවුඩ බිඳ දැමීමට හැකි වූ නිසයි ( A වෙනුවට 4, B වෙනුවට 5 ආකාරයෙන් ).[8]
2011 වසරේදී රජීබ් කරීම් එක්සත් රාජ්ය්යෙදී ත්රස්තවාද අපරාධ සඳහා වරදකරු බවට පත් විය. වරද වූයේ බංගලාදේශයේ ඉස්ලාමික ක්රියාකාරීන් පිරිසක් සමඟ බ්රිතාන්ය්ය ගුවන් තොටුපළ පුපුරා විනාශ කිරීමට හා එහි තොරතුරු තාක්ෂණ ජාලය කඩාකප්පල් කිරීමට සාකච්ඡා කිරීමය. ඔවුන්ට මීට වඩා දියුණු කේතාංක ක්රම භාවිතා කළ හැකි වූවත් ඒවායේ ආරක්ෂාව අඩුයි සිතා ඔවුන් ඔවුන්ගේ ක්රමයම යොදා ගෙන ඇත.[9]
කේතාංකය බිඳදැමීම
[සංස්කරණය]| ප්රතිකේතන මාරුව | අපේක්ෂිත සරල පාඨය |
|---|---|
| 0 | exxegoexsrgi |
| 1 | dwwdfndwrqfh |
| 2 | cvvcemcvqpeg |
| 3 | buubdlbupodf |
| 4 | attackatonce |
| 5 | zsszbjzsnmbd |
| 6 | yrryaiyrmlac |
| … | |
| 23 | haahjrhavujl |
| 24 | gzzgiqgzutik |
| 25 | fyyfhpfytshj |
කේතාංක පෙළ පමණක් ඇති අවස්ථාවේ වූවත්, මෙම සීසර් කේතාංකය බිඳ දැමීම පහසු වේ. මෙය ආකාර දෙකකින් විය හැක:
- හරියාකාරයෙන්ම සීසර් රීතිය යොදා ඇති බව නොදැන, නමුත් කිසියම් ආකරයේ සරල ප්රතිස්ථාපන කේතාංක ක්රමයක් යොදා ඇති බව දැන හෝ අනුමාන කර පද්ධතියට පහර දීම.
- සීසර් කේතාංකය භාවිතා කර ඇති බව දන්නා වූවත් එහි ප්රතිස්ථාපන අගය නොදැන පත්ධතියට පහර දීම.
පළමු අවස්ථාවේදී, සංඛ්යාත විශ්ලේෂණය හෝ රටා වචන වැනි ප්රතිස්ථාපන කේතාංකයක යොදා ගන්නා සාමාන්ය සරල ක්රමයක් භාවිතයෙන් බිඳ දැමිය හැක.[10] බොහෝ විට පහර දෙන්නා විසින් මෙහි ඇති සවිධිතාව බව ඉක්මණින් හඳුනා ගෙන, එහි සීසර් කේතාංකය යොදා ඇති බවට අනුමාන කරයි.
දෙවන අවස්ථාවේදී බිඳ දැමීම ඉහත අවස්ථාවට වඩා පහසු වේ. බෘට් ෆෝස් පහර දීමක්[11] මගින් විය හැකි සීමා සහිත ප්රතිස්ථාපන අවස්ථා(ඉංග්රිසි හෝඩියේ 26 යි ) හඳුනා ගත හැක. විය හැකි අවස්ථා සියල්ලටම කේතාංකයේ කුඩා කොටසක් වගු ගත කිරීමෙන් ද මෙය කළ හැක.[12] එම ක්රමය සාමාන්ය කොටස සම්පූර්ණ කිරීම ලෙස හැඳින්වේ.[13] මෙහි දක්වා ඇති කේතාංක පෙළේ කොටසේ "EXXEGOEXSRGI"; සාමාන්ය අක්ෂර පෙළ (ක්ෂණිකව ප්රතිස්ථාපන හතරක් මගින්) හඳුනාගත හැකි වේ. කේතාංක පෙළේ සෑම අකුරක් යටින්, එම අකුරින් පටන් ගන්නා ලෙසට මුළු අක්ෂර මාලාවම ආපසු අතට ලිවීමෙන් ද මෙය සිදු කර ගත හැකි වේ. පෙර කියූ පරිදි අක්ෂර මාලාව ආපසු අතට ලියූ තීරු භාවිතාකර මෙම ක්රමය ඉක්මන් කර ගත හැකි වේ. කේතාංකයේ පිළිවෙලට එම තීරු තැබූ විට, පණිවුඩය වෙනත් පෙළක දැකගත හැකි වේ.
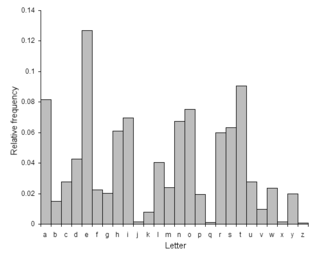
අක්ෂරවල සංඛ්යාත ව්යාප්තිය ගැලපීම තවත් බ්රෘට් ෆෝස් ප්රවේශයක් ලෙස හඳුනා ගත හැක. සාමාන්ය පුද්ගලයෙකුට ඉතා පහසුවෙන් කේතාංකයේ අක්ෂරවල සංඛ්යාත වගුගත කිරීමෙන් සහ සාමාන්ය අක්ෂර පෙළේ එම අකුරුවල අපේක්ෂිත ව්යාප්තිය දන්නේ නම් වගුවේ සුවිශේෂ ලක්ෂණවල වෙනස් වීම් අධ්යයනයෙන් ද ප්රතිස්ථාපන අගය සොයාගත හැකි වේ. මෙය සංඛ්යාත විශ්ලේෂණය ලෙස හැඳින්වේ. උදාහරණයක් ලෙස ඉංග්රීසි භාෂාවේ E, T (ඉතා බහුල ) සහ Q, Z(ඉතා අඩුවෙන්ම ) ව්යාප්තිය එකිනෙකට වෙනස් වේ.[14] කොතරම් දුරට අපෙක්ෂිත ව්යාප්තිය සහ සැබෑ ව්යාප්තිය ගැලපෙනවා දැයි සෙවීමෙන් පරිඝනකයකට වූවද මෙය සිදුකර හැක.උදාහරණයක් ලෙස 'කයි වර්ග ව්යාප්තියක්' මේ සඳහා යොදාගත හැක.[15]
ස්වභාවික භාෂාවේ හුදු පෙළේ විය හැකි සෑම අවස්ථාවකටම වාගේ ඇත්තේ පිළිගත හැකි එක විකේතන ක්රමයයි. නමුත් අතිශයින් කුඩා හුදු පෙළ සඳහා ක්රම බොහෝ ගණනක් ඇත. උදාහරණයක් වශයෙන් MPQY කේතාංක පෙළ "aden" හෝ "know"(සාමාන්ය අක්ෂර පෙළ ඉංග්රීසි ලෙස උපකල්පනය කිරීමෙන් ) ලෙසටද "ALIIP" "dolls" හෝ "wheel" ලෙසටද "AFCCP" "jolly" හෝ "cheer" ලෙසටද පැහැදිලිව තේරුම්ගත හැකිවේ.
විවිධ කේතාංක හෝ විකේතන ක්රම භාවිතායෙන් අමතර ආරක්ෂාවක් සැලසිය නොහැකි වේ. එයට හේතුවනම් ප්රතිස්ථාපනය A අගයකින් ඉන්පසුව B අගයකින් ලැබෙන පිළිතුර A + B ප්රතිස්ථාපනයට සමාන වීමය. කේතාංකය විවිධ අගයන් මගින් ලබාගත් විට එම අගයන් සමූහව කණ්ඩායම් සාදයි.[16]
සටහන
[සංස්කරණය]- ^ Luciano, Dennis (1987). "Cryptology: From Caesar Ciphers to Public-Key Cryptosystems". The College Mathematics Journal. 18 (1): 2–17. doi:10.2307/2686311. JSTOR 2686311.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help); Unknown parameter|month=ignored (help) - ^ Wobst, Reinhard (2001). Cryptology Unlocked. Wiley. p. 19. ISBN 978-0-470-06064-3.
- ^ Pieprzyk, Josef (2003). Fundamentals of Computer Security. Springer. p. 6. ISBN 3-540-43101-2.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Kahn, David (1967). The Codebreakers. pp. 775–6. ISBN 978-0-684-83130-5).
{{cite book}}: Check|isbn=value: invalid character (help) - ^ Kahn, David (1967). The Codebreakers. pp. 631–2. ISBN 978-0-684-83130-5).
{{cite book}}: Check|isbn=value: invalid character (help) - ^ Wobst, Reinhard (2001). Cryptology Unlocked. Wiley. p. 20. ISBN 978-0-470-06064-3.
- ^ Kahn, David (1967). The Codebreakers. ISBN 978-0-684-83130-5).
{{cite book}}: Check|isbn=value: invalid character (help) - ^ Leyden, John (2006-04-19). "Mafia boss undone by clumsy crypto". The Register. සම්ප්රවේශය 2008-06-13.
{{cite news}}: Italic or bold markup not allowed in:|publisher=(help) - ^ "BA jihadist relied on Jesus-era encryption". The Register. 2011-03-22. සම්ප්රවේශය 2011-04-01.
{{cite news}}: Italic or bold markup not allowed in:|publisher=(help) - ^ Beutelspacher, Albrecht (1994). Cryptology. Mathematical Association of America. pp. 9–11. ISBN 0-88385-504-6.
- ^ Beutelspacher, Albrecht (1994). Cryptology. Mathematical Association of America. pp. 8–9. ISBN 0-88385-504-6.
- ^ Leighton, Albert C. (1969). "Secret Communication among the Greeks and Romans". Technology and Culture. 10 (2): 139–154. doi:10.2307/3101474. JSTOR 3101474.
{{cite journal}}: Unknown parameter|month=ignored (help) - ^ Sinkov, Abraham (1966). Elementary Cryptanalysis: A Mathematical Approach. Mathematical Association of America. pp. 13–15. ISBN 0-88385-622-0.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Singh, Simon (2000). The Code Book. Anchor. pp. 72–77. ISBN 0-385-49532-3.
- ^ Savarese, Chris (2002-07-15). "The Caesar Cipher". සම්ප්රවේශය 2008-07-16.
{{cite web}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Wobst, Reinhard (2001). Cryptology Unlocked. Wiley. p. 31. ISBN 978-0-470-06064-3.
ග්රන්ථ නාමාවලිය
[සංස්කරණය]- David Kahn, The Codebreakers — The Story of Secret Writing, 1967. ISBN 0-684-83130-9.
- F.L. Bauer, Decrypted Secrets, 2nd edition, 2000, Springer. ISBN 3-540-66871-3.
- Chris Savarese and Brian Hart, The Caesar Cipher, 1999
බාහිර සම්බන්ධක
[සංස්කරණය]- Weisstein, Eric W. "Caesar's Method". MathWorld.
- The Caesar Shift සංරක්ෂණය කළ පිටපත 2007-10-19 at the Wayback Machine discussed on The Beginner's Guide to Cryptography සංරක්ෂණය කළ පිටපත 2012-01-11 at the Wayback Machine
- A simple approach to crack a Caesar cipher


