ත්‍රිකෝණමිතික ශ්‍රිත

ගණිතයේදී, ත්‍රිකෝණමිතික ශ්‍රිත (වෘත්තාකාර ශ්‍රිත ලෙසද හැඳින්වේ) යනු කෝණයක ශ්‍රිත වේ. ඒවා භාවිතා වන්නේ ත්‍රිකෝණයක කෝණ ත්‍රිකෝණයෙහි පැතිවල දිගට අදාළ කිරීමටය. වෙනත් බොහෝ භාවිතා අතර, ත්‍රිකෝණ පිළිබඳ හැදෑරීමට සහ ආවර්තික සංසිද්ධින් ආදෘශ්‍යනය කිරීමට ත්‍රිකෝණමිතික ශ්‍රිත වැදගත් වෙයි.

ත්‍රිකෝණමිතික ශ්‍රිත පොදුවේ, කෝණය අඩංගු වන සෘජුකෝණි ත්‍රිකෝණයක පාද දෙකක දිග අතර අනුපාතයක් ලෙස අර්ථ දැක්විය හැකිය. එසේම ඒකක වෘත්තයක සිට විවිධ රේඛා කාණ්ඩවල දිග ලෙසද අර්ථ දැක්විය හැකිය. බොහෝ නවීන අර්ථ කථනයන් මගින් එය අපරිමිත ‍ශ්‍රේණි ලෙස හෝ අභිමත ධන හෝ සෘණ අගයන්ට හා සංකීර්ණ සංඛ්‍යාවලට පවා විස්තාරණය වූ අවල්‍ය සමීකරණවල විසඳුම් ලෙස වඩාත් පුළුල් ලෙස දැක්විය හැකිය.

සෘජුකෝණී ත්‍රිකෝණික නිර්වචන

A නැමති කෝණය අඩංගු අභිමත සෘජුකෝණි ත්‍රිකෝණයක, A කෝණය සඳහා ත්‍රිකෝණමිතික ශ්‍රිත අර්ථ දැක්වීමේදී, ත්‍රිකෝණයේ පාද සදහා පහත සඳහන් නම් යොදා ගනී.

කර්ණය යනු සෘජුකෝණයට ප්‍රතිවිරුද්ධ පාදය හෝ සෘජුකෝණී ත්‍රිකෝණයේ දිගම පාදය යැයි නිර්වචනය කරයි. මෙය h ලෙස ගනී.
සම්මුඛ පාදය යනු අප භාවිතා කරන කෝණයට ප්‍රතිවිරුද්ධ පාදයයි. මෙය a ලෙස ගනී.
බද්ධ පාදය යනු අප භාවිතා කරන කෝණය හා සෘජු කෝණය යන දෙකම අඩංගු වන පාදයයි. මෙය b ලෙස ගනී.

සියලු ත්‍රිකෝණ ගනු ලබන්නේ යුක්ලීඩ් තලයේ පවතින පරිදි වේ. ඒනිසා සෑම ත්‍රිකෝණයකම අභ්‍යන්තර කෝණවල ඓක්‍යය රේඩියන් π (1800) වේ. මේ නිසා සෘජුකෝණි ත්‍රිකෝණවල සෘජු කෝණි නොවන ඉතිරි කෝණ රේඩියන් 0 හා π (900) අතර පිහිටයි. කියවන්නා විසින් සැලකිය යුතු කරුණ නම් නිරතුරුවම, ත්‍රිකෝණමිතික ශ්‍රිත අර්ථ දැක්වීමේදී කෝණය මෙම පරාසය තුළ තිබෙන බවයි. ඒකක වෘත්තයක් යොදාගෙන හෝ සමමිතියක් සැලකීමෙන් හා ආවර්තිත ශ්‍රිතයක් ලෙස සලකමින් අපට මෙය සම්පූර්ණ තර්කයක් බවට විස්තීරණය කළ හැක.

ශ්‍රිත සංක්ෂේපණ සර්ව සාම්‍යයන්

(රේඩියන් මගින්)

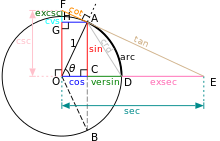
කෝණයක සියළු ත්‍රිකෝණමිතික ශ්‍රිතයන් කේන්ද්‍රය 0 වන වෘන්තයක පාදයන් මගින් ජ්‍යාමිතිකව ගොඩනැගිය හැකිය.

නවීන ව්‍යවහාරයේදී වගුගත කොට ඇති එකිනෙකට සම්බන්ධ සමීකරණ සමග මූලික ත්‍රිකෝණමිතික ශ්‍රිතයන් හයක් භාවිතා කරයි. විශේෂයෙන් අවසන් ශ්‍රිත හතරේ එම සම්බන්ධතා බොහෝ විට ගනු ලබන්නේ මුල් ශ්‍රිත දෙකේ නිර්වචන මගිනි. නමුත් ඒවා ජ්‍යාමිතිකව ගොඩනැගිය හැකිය.

ප්‍රතිලෝම ශ්‍රිත

ත්‍රිකෝණමිතික ශ්‍රිත ආවර්තක වන අතර මේ නිසා ආක්ෂේපක නොවේ. එනිසා ඒවාට එම ආකාරයෙන්ම ප්‍රතිලෝම ශ්‍රිත නොමැත. එම නිසා ප්‍රතිලෝම ශ්‍රිත අර්ථ කථනය සඳහා ඒවා සාපේක්ෂ වන පරිදි වසම් සීමා කළ යුතු වේ. පහත සඳහන් ඒවාවල වම්පස ඇති ශ්‍රිත දකුණු පස ඇති සමීකරණ මගින් අර්ථ දක්වන අතර මේවා සාධනය කලහැකි සර්ව සාම්‍යයන් නොවේ. ප්‍රධාන ප්‍රතිලෝම ශ්‍රිත පහත පරිදි අර්ථ දක්වයි.

{\begin{matrix}{\mbox{for}}&-{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}},&y=\arcsin x&{\mbox{if}}&x=\sin y\,;\\\\{\mbox{for}}&0\leq y\leq \pi ,&y=\arccos x&{\mbox{if}}&x=\cos y\,;\\\\{\mbox{for}}&-{\frac {\pi }{2}}<y<{\frac {\pi }{2}},&y=\arctan x&{\mbox{if}}&x=\tan y\,;\\\\{\mbox{for}}&-{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}},y\neq 0,&y=\operatorname {arccsc} x&{\mbox{if}}&x=\csc y\,;\\\\{\mbox{for}}&0\leq y\leq \pi ,y\neq {\frac {\pi }{2}},&y=\operatorname {arcsec} x&{\mbox{if}}&x=\sec y\,;\\\\{\mbox{for}}&0<y<\pi ,&y=\operatorname {arccot} x&{\mbox{if}}&x=\cot y\,.\end{matrix}}

ප්‍රතිලෝම ත්‍රිකෝණමිතික ශ්‍රිතවලදී බොහෝ විට චාප සයින, චාප කොසයින යනාදිය සඳහා sin⁻¹ සහ cos⁻¹ අංකනය බහුලව ලෙස භාවිතා කෙරේ. මෙම අංකනය යොදාගන්නා විට ශ්‍රිතවල ගුණන ප්‍රතිලෝම සමග ප්‍රතිලෝම ශ්‍රිත පැටලිය හැක. "arc-" උපසර්ගය භාවිතා කරන අංකනය එවැනි පැටලුම් ඇති නොකරන නමුත් "arcsec" යන්න "arcsecond" සමග පැටලිය හැක. sin හා cos ලෙසම ප්‍රතිලෝම ත්‍රිකෝණමිතික ශ්‍රිතද අපරිමිත ශ්‍රේණි මගින් දැක්විය හැක. නිදසුනක් වශයෙන්,