පරිපූර්ණ වායු (ප්‍රත්‍යාවර්ථ අවස්ථාව)

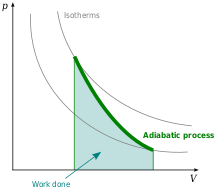
සරල ද්‍රව්‍යයක් මත ක්‍රියා කරන ස්ථිරතාපී ක්‍රියාවලියක් නිසා පරිමා වැඩිවීමක් සිදුවේ නම් ක්‍රියාකාරී ද්‍රව්‍යයේ අභ්‍යන්තර ශක්තිය අත්‍යාවශ්‍යයෙන්ම පහල යයි.

ප්‍රතිවර්ත්‍ය ස්ථිර තාපී ක්‍රියාවලියකට යටත් වන පරිපූර්ණ තරලයක් සඳහා (මෙහිදී එන්ට්‍රොපි ජනනයක් සිදු නොවේ) ගණිතමය සමීකරණය පහත දැක්වේ.

$PV^{\gamma }=\operatorname {constant} \qquad$

මෙහි P යනු පීඩනය ද, V යනු පරිමාව ද වන අතර

$\gamma ={C_{P} \over C_{V}}={\frac {\alpha +1}{\alpha }},$

මෙහි $C_{P}$ යනු නියත පීඩනය යටතේ විශිෂ්ට තාපය ද, $C_{V}$ යනු නියත පරිමා තත්ව යටතේ විශිෂ්ට තාපය ද වේ. වැසුමේ නිදහස් භාවයේ අංශක සංඛ්‍යාව 2න් බෙදූ විට $\alpha$ ලැබේ. (ඒක පරමාණුක වායු සඳහා 3/2, ද්වී පරමාණුක වායු සඳහා 5/2) මේ අනුව එක් පරමාණුක පරිපූර්ණ වායුවක් සඳහා $\gamma =5/3$ ද ද්වී පරමාණුක වායුවක (වාතයේ ප්‍රධාන සංඝටක වන නයිට්‍රජන් හෝ ඔක්සිජන් වැනි වායු) සඳහා $\gamma =7/5$ ද වේ. කෙසේ නමුත් මෙම සූත්‍ර‍යන් පෞරාණික භෞතික විද්‍යාවේ දී සලකනු ලබන පරිපූර්ණ වායු සඳහා පමණක් වලංගු වන අතර බෝස් - අයින්ස්ටයින් හෝ ෆර්මි වායූන් සඳහා යෙදිය නොහැක.

T යනු නිරපේක්ෂ උෂ්ණත්වය වේ නම්, ප්‍රතිවර්ත්‍ය ස්ථිරතාපී ක්‍රියාවලියක් සඳහා

$P^{\gamma -1}T^{-\gamma }=\operatorname {constant}$

$VT^{\alpha }=\operatorname {constant}$

යන සමීකරණ යුගලය ද සත්‍ය වේ.

මෙය පහත පරිදි ද ලිවිය හැක.

$TV^{\gamma -1}=\operatorname {constant}$

සන්තතික සූත්‍රය ව්‍යුත්පන්න කිරීම

ස්ථිරතාපී ක්‍රියාවලියක් අර්ථ දැක්වීමේ දී පද්ධතිය සඳහා තාප හුවමාරුව ශුන්‍ය වේ යැයි (δQ = 0) යැයි කියනු ලැබේ. එවිට තාප ගති විද්‍යාවේ පළමු නියමය ඇසුරින් පහත සමීකරණය ලබා ගත හැක.

${\text{(1)}}\qquad dU+\delta W=\delta Q=0$

මෙහි dU යනු පද්ධතියේ අභ්‍යන්තර ශක්ති වෙනස වන අතර δW යනු පද්ධතිය මඟින් කෙ‍රුණු කාර්යය වේ. ‍බාහිරින් පද්ධතිය වෙත ශක්තිය ලැබීමත් (δQ) සිදු නොවන බැවින් පද්ධතිය මඟින් සිදු කරන ඕනෑම කාර්යයක් δW සඳහා එහි අභ්‍යන්තර ශක්තිය (U) වැය කළ යුතුය. පද්ධතිය මඟින් සිදු කළ පීඩන - පරිමා කාර්යය (δW) පහත ලෙස අර්ථ දැක්විය හැක.

${\text{(2)}}\qquad \delta W=-P\,dV.$

කෙසේ නමුත් ස්ථිරතාපී ක්‍රියාවලියක් තුළ දී P නියතව නොපවතින අතර ඒ වෙනුවට එය V සමඟ විචලනය වේ. ස්ථිරතාපී ක්‍රියාවලිය ක්‍රියාත්මක වීමේ දී dP හා dV අගයන් අතර පවතින සම්බන්ධය දැන සිටීම අවශ්‍ය වේ. පරිපූර්ණ වායුවක් සඳහා අභ්‍යන්තර ශක්තිය පහත සමීකරණය මඟින් දෙනු ‍ලැබේ.

${\text{(3)}}\qquad U=\alpha nRT$

මෙහි R යනු සර්වත්‍ර වායු නියතයද, n යනු පද්ධතිය තුළ අඩංගු මවුල සංඛ්‍යාවද (නියතයකි)වේ. ඉහත (3) සමීකරණ අවකලනය කිරීමෙන් සහ එය පරිපූර්ණ වායු නියමය , PV = nRT යෙදීමෙන්,

${\text{(4)}}\qquad dU=\alpha nR\,dT=\alpha \,d(PV)=\alpha (P\,dV+V\,dP).$

යන සමීකරණය ලැබෙන අතර, මෙම (4) වැනි සමීකරණය බොහෝ විට $dU=nC_{V}\,dT$ යනුවෙන් ප්‍රකාශ කෙරේ. $C_{V}=\alpha R$ වීම එයට හේතුවයි. දැන් (1) සමිකරණයට (2) සහ (4) යන සමීකරණ ආදේශයෙන් පහත සමීකරණය ලබා ගත හැක.

$-P\,dV=\alpha P\,dV+\alpha V\,dP\,$

මෙය තවදුරටත් සරල කළ විට ,

$-(\alpha +1)P\,dV=\alpha V\,dP\,$ යන සමීකරණය ලැබේ.

දැන් මෙහි දෙපසම PV මඟින් බෙදූ විට පහත සමීකරණය ලබා ගත හැක.

$-(\alpha +1){dV \over V}=\alpha {dP \over P}.$

සමීකරණයේ වම් පස සහ දකුණු පස V0 සිට V ට සහ P0 සිට P ට අනුකලනය කර පදයන්හි පිහිටුම අතුරුමාරු කිරීමෙන්,

$\ln \left({P \over P_{0}}\right)={-{\alpha +1 \over \alpha }}\ln \left({V \over V_{0}}\right).$ යන සමීකරණය ලැබේ.

දෙපසම ඝාතීයකරණය කරන්න.

$\left({P \over P_{0}}\right)=\left({V \over V_{0}}\right)^{-{\alpha +1 \over \alpha }},$

අනතුරුව ඍණ ලකුණ ඉවත් කිරීමෙන් පහත සමීකරණය ලබා ගත හැක.

$\left({P \over P_{0}}\right)=\left({V_{0} \over V}\right)^{\alpha +1 \over \alpha }.$

ඒ අනුව,

$\left({P \over P_{0}}\right)\left({V \over V_{0}}\right)^{\alpha +1 \over \alpha }=1$ ද

$PV^{\alpha +1 \over \alpha }=P_{0}V_{0}^{\alpha +1 \over \alpha }=PV^{\gamma }=\operatorname {constant} .$ ද වේ.

විවික්ත සූත්‍රය ව්‍යුත්පන්න කිරීම, පද්ධතිය 1 අවස්ථාවේ සිට 2 අවස්ථාව දක්වා මනින ලද ශක්ති වෙනස

${\text{(1)}}\qquad \delta U=\alpha Rn_{2}T_{2}-\alpha Rn_{1}T_{1}=\alpha R(n_{2}T_{2}-n_{1}T_{1})$ ට සමාන වේ.

ඊට සමගාමීව එම ක්‍රියාවලියේ ප්‍රතිඵලයක් ලෙස සිදුවන පීඩන පරිමා වෙනස්කම් නිසා සිදුවන කාර්යය ප්‍රමාණය

${\text{(2)}}\qquad \delta W=P_{2}V_{2}-P_{1}V_{1}$ ට සම වේ.

කෙසේ නමුත් ක්‍රියාවලිය ස්ථිරතාපී විය යුතු බැවින් පහත සමීකරණය ද සත්‍ය වේ.

${\text{(3)}}\qquad \delta U+\delta W=0$

(1) හා (2) සමීකරණ 3හි අදේශ කළ විට ප්‍රතිඵලය ලෙස පහත සමීකරණ යුගලෙන් 1ක් ලබා ගත හැක.

$\alpha R(n_{2}T_{2}-n_{1}T_{1})+(P_{2}V_{2}-P_{1}V_{1})=0\qquad \qquad \qquad$

හෝ

${\frac {(P_{2}V_{2}-P_{1}V_{1})}{-(n_{2}T_{2}-n_{1}T_{1})}}=\alpha R\qquad \qquad \qquad$

මවුලීය ප්‍රමාණයෙහි වෙනසක් සිදු නොවේ යැයි උපකල්පනය කරයි නම් (බොහෝ විට ප්‍රායෝගික තත්වය යටතේ මෙය සත්‍ය වේ) සමීකරණය පහත පරිදි තවදුරටත් සරල කළ හැක.

${\frac {(P_{2}V_{2}-P_{1}V_{1})}{-(T_{2}-T_{1})}}=\alpha nR\qquad \qquad \qquad$

http://en.wikipedia.org/wiki/Adiabatic_process#Ideal_gas_.28reversible_case_only.29