සමාන්තරාස්රය
Appearance
| සමාන්තරාස්රය | |
|---|---|
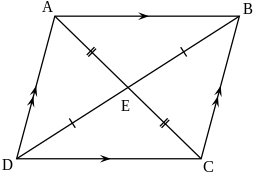 මෙම සමාන්තරාස්රය රොම්බාභයක් වන්නේ එහි කෝණ සියල්ල ඇල කෝණ නිසාවෙනි. | |
| වර්ගය | චතුරස්රය |
| දාර සහ ශීර්ෂ | 4 |
| සමමිතික කාණ්ඩය | C2 (2) |
ජ්යාමිතියෙහි, සමාන්තරාස්රයක් යනු සමාන්තර පැති යුගලයක් සහිතවූ චතුරස්රයකි. යුක්ලිඩියානු ජ්යාමිතියෙහි, සමාන්තරාස්රයක සම්මුඛ හෝ අභිමුඛ පාදයන් සමාන දිගින් යුතු වන අතර සමාන්තරාස්රයක සම්මුඛ කෝණ සමාන අගයයකින් යුකු වෙති. සම්මුඛ පාදයන්ගේ හා සම්මුඛ කෝණයන්ගේ අංගසාම්යය, යුක්ලිඩියානු සමාන්තර මූලසත්යයෙහි සෘජු ප්රතිඵලයක් වන අතර, යුක්ලිඩියානු සමාන්තර මූලසත්යයේ හෝ එහි තුල්ය සූත්රකරණයක උපකාරීත්වයෙන් තොරව, මෙම නියමයන් දෙකෙන් එකක් හෝ සාධනය කල නොහැකි වෙයි. සමාන්තරාස්රයක ත්රිමාන ප්රතිරූපය සමාන්තරානීකය වෙයි.
පදයෙහි ශබ්ද නිරුක්තිය (ග්රීක බසින් παραλληλ-όγραμμον, "සමාන්තර රේඛා වලින් සමන්විත" හැඩයක්) මෙහි අර්ථදැක්වීම අනුමත කරයි.
ගුණංග
[සංස්කරණය]- සමාන්තරාස්රයක සම්මුඛ පාද සමාන දිගකින් යුතු වෙති.
- සමාන්තරාස්රයක සම්මුඛ කෝණ සමාන අගයයකින් යුතු වෙති.
- බද්ධ කෝණ e පරිපූරක වෙති (එකතුව අංශක 180 ට සමාන වෙයි).
- සමාන්තරාස්රයක වර්ගඵලය, , වන්නේ වන අතර, එහි යනු සමාන්තරාස්රයෙහි ආධාරකය වන අතර යනු එහි උස වෙයි.
- සමාන්තරාස්රයක සම්මුණ පාද සමාන්තර (අර්ථදැක්වීම ප්රකාර) වන අතර කිසි විටෙක් ඡේදනය නොවෙති.
- සමාන්තරාස්රයක වර්ගඵලය එහි එක් විකර්ණයකින් සැදෙන ත්රිකෝණයක වර්ගඵලය මෙන් දෙගුණයකි.
- සමාන්තරාස්රයක වර්ගඵලය එහි බද්ධ පාදයන් දෙකක දෛශික කතිර ගුණිතයෙහි විශාලත්වයට සමාන වෙයි.
- සමාන්තරාස්රයක විකර්ණයන් එකිනෙක සමච්ඡේද කරති.
- පරිහීන-නොවන ඕනෑම ආබඳන පරිණාමනයක් විසින් සමාන්තරාස්රයක් තවත් සමාන්තරාස්රයක් බවට පත් කරයි.
කිසියම් සමාන්තරාස්රයක් චතුරස්රයක් බවට පත් කල හැකි ආබඳන පරිණාමනයන් අනන්ත සංඛ්යාවක් ඇත . - සමාන්තරාස්රයක් සඳහා දෙවන ගණයේ භ්රමණ සමමිතියක් ඇත (180° කින් වෙනස් වන). එය සඳහා පරාවර්තන සමමිතිය සහිත රේඛා දෙකක් ද පැවතීමට නම් එය රොම්බසයක් හෝ සෘජු කෝණෘස්රයක් හෝ විය යුතුය.
- සමාන්තරාස්රයක පරිමිතිය වන්නේ 2(a + b) වන අතර මෙහි a සහ b යනු බද්ධ පාදයන්හී දිග වෙති




