 පාදවල දිග අනුයාත ෆිබොනාච්චි සංඛ්යාවලට අනුරූප වන ආකාරයේ සමචතුරස්ර ඇසුරින් කළ ඇතිරුමක් ඉහත දැක්වේ
පාදවල දිග අනුයාත ෆිබොනාච්චි සංඛ්යාවලට අනුරූප වන ආකාරයේ සමචතුරස්ර ඇසුරින් කළ ඇතිරුමක් ඉහත දැක්වේ
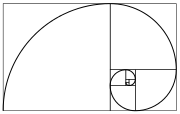 ඉහත දක්වා ඇති ඇතිරුමෙහි සමචතුරස්රයන්හි ප්රතිවිරුද්ධ ශීර්ෂ යා කරමින් චාප ඇඳීම මඟින් නිර්මාණය කරගත් ෆිබොනාච්චි සර්පිලය මෙහි දැක්වේ; මෙය භාවිතා කරන්නේ 1, 1, 2, 3, 5, 8, 13, 21, සහ 34 යන ප්රමාණයේ සමචතුරස්ර වෙති. - රන්මය සර්පිලය බලන්න.
ඉහත දක්වා ඇති ඇතිරුමෙහි සමචතුරස්රයන්හි ප්රතිවිරුද්ධ ශීර්ෂ යා කරමින් චාප ඇඳීම මඟින් නිර්මාණය කරගත් ෆිබොනාච්චි සර්පිලය මෙහි දැක්වේ; මෙය භාවිතා කරන්නේ 1, 1, 2, 3, 5, 8, 13, 21, සහ 34 යන ප්රමාණයේ සමචතුරස්ර වෙති. - රන්මය සර්පිලය බලන්න.
ගණිතයෙහි, ෆිබොනාච්චි සංඛ්යා හෝ ෆිබොනාච්චි අනුක්රම හෝ ෆිබොනාච්චි ශ්රේණි යනු පහත නිඛිල අනුක්රමය අනුගමනය කරන සංඛ්යා වෙයි:
 (OEIS හි A000045 අනුක්රමය)
(OEIS හි A000045 අනුක්රමය)
හෝ, විකල්ප වශයෙන්,[1]

අර්ථ දැක්වීම අනුව, ෆිබොනාච්චි අනුක්රමයෙහි පළමු සංඛ්යා දෙක 0 සහ 1 (විකල්ප වශයෙන්, 1 සහ 1) වන අතර, එක් එක් අනුයාත සංඛ්යාව පෙර සංඛ්යා දෙකෙහි එකතුව වෙයි.
ගණිතමය භාෂිතය අනුව, Fn යන ෆිබොනාච්චි සංඛ්යා අනුක්රමය අර්ථ දැක්වෙන්නේ පහත පුනරාවර්තන සම්බන්ධය පරිදීය

මෙහ සන්තති අගයයන්[2]
පළමු ආකාරයෙහිදී

වන අතර, දෙවන ආතාරයෙහිදී

වෙයි.
ෆිබොනාච්චි ලෙසින්ද හැඳින්වුනු පීසාහී ලියොනාර්ඩෝ අනුව යමින් ෆිබොනාච්චි අනුක්රමය නම් තබා ඇත. පෙරදී ඉන්දියානු ගණිතයෙහි මෙම අනුක්රමය විස්තර කර තුබුණද, ෆිබොනාච්චිගේ 1202 ග්රන්ථය ලිබර් අබාසි තුලින් මෙම අනුක්රමය බටහිර යුරෝපීය ගණිතය වෙතට හඳුන්වා දෙන ලදි [3].
[3]
- ↑ නිදසුනක් ලෙසින් බෙක් සහ ජියෝජෙගාන් (2010), හෝ බෝනා (2011), පිටුව 180.
- ↑ ලූකස් පි. 3
- ↑ 3.0 3.1 සිග්ලර් (පරි.) (2002), පරිච්ඡේදය II.12, පිටු. 404–405.







