සූදකු


සූදකු (数独 sūdoku?) ![]() සවන්දෙන්න (උදවු·විස්තර) යනු කර්ක ශාස්ත්රය-පදනම් කොටගෙන සංඛ්යා ස්ථානගත කිරීමේ ප්රහේලිකාවකි. මෙහි පරමාර්ථය වනුයේ 9×9 ජාලකයක්, එක් එක් සිරස් පේළිය, එක් එක් තිරස් පේළිය හා එක් එක් 3×3 කොටු නවය (කොටස හෝ පෙදෙස ලෙසද හැඳින්වේ)තුල අංක 1 සිට 9 දක්වා එක් වරක් පමණක් අඩංගු වන පරිදි සම්පූර්ණ කිරීමය. ප්රහේලිකාව සකස්කොට ඉදිරිපත් කරන්නා විසින් භාගික වශයෙන් සම්පූර්ණ ජාලකයක් සපයනු ලැබේ.
සවන්දෙන්න (උදවු·විස්තර) යනු කර්ක ශාස්ත්රය-පදනම් කොටගෙන සංඛ්යා ස්ථානගත කිරීමේ ප්රහේලිකාවකි. මෙහි පරමාර්ථය වනුයේ 9×9 ජාලකයක්, එක් එක් සිරස් පේළිය, එක් එක් තිරස් පේළිය හා එක් එක් 3×3 කොටු නවය (කොටස හෝ පෙදෙස ලෙසද හැඳින්වේ)තුල අංක 1 සිට 9 දක්වා එක් වරක් පමණක් අඩංගු වන පරිදි සම්පූර්ණ කිරීමය. ප්රහේලිකාව සකස්කොට ඉදිරිපත් කරන්නා විසින් භාගික වශයෙන් සම්පූර්ණ ජාලකයක් සපයනු ලැබේ.
විසඳා හමාර කරන ලද සූදකු ප්රහේලිකා ලතින් කොටු ගණයට අයත් වන මුත්, එක් එක් කොටස් හෝ ප්රදේශ වල අන්තර්ගතය පිළිබඳ පැනවුනු අමතර සංරෝධනයන් හේතුවෙන් ලතින් කොටු වලින් වෙනස් වේ. ලියොනාඩ් ඉයුලර් මෙම ප්රහේලිකාවේ නිර්මාතෘ ලෙස සාවද්ය ලෙස උපුටා දැක්වෙනුයේ ලතින් කොටු සම්බන්ධයෙන් ඔහු විසින් සිදුකරන ලද ගණනයන්, විශ්ලේෂණ හා පර්යේෂණ හේතුවෙනි. .[1]
නූතන ප්රහේලිකාව, ඇමරිකානු වාස්තුවිද්යාඥ හොවාඩ් ගාන්ස් වෙතින් 1979 දී නිමැවී ඩෙල් සඟරා හි "අංක පෙදෙස" යන නම යටතේ ප්රකාශයට පත් විය. [2] මෙය 1986 දී ජපානයේ ජනප්රිය භාවයට පත් වූයේ, නිකෝලි විසින් ප්රකාශයට පත්කරනු ලැබ, තනි අංකය යන අරුත් දනවන සූදකු යන නම ආරූඨ කිරීමෙන් අනතුරුවය.[3] එය 2005 දී ජාත්යන්තර ජනමෝදකයක් බවට පත් විය.
හැඳින්වීම[සංස්කරණය]
සූදකු (数独) යන නාමය "සූජි වා දකුෂින් නි කගිරු" යනුවෙන් උච්චාරණය වන හා "සංඛ්යා හුදකලා විය යුතුයි", හෝ "සංඛ්යා එක් වරක් පමණක් භාවිත විය යුතුයි" යනුවෙන් අරුත් දනවන "数字は独身に限る" යන්නට කෙටි පදයයි. [4] මෙම නාමය ප්රහේලිකාවේ ප්රකාශක ජපානයේසීමාසහිත නිකෝලි සමාගමේ වෙළෙඳ ලකුණක් වේ .[4] ජපන් බසින්, මෙම වචනය උච්චාරණය වනුයේ සැකිල්ල:IPA2 ලෙසය; ඉංග්රීසියෙන්, එය සාමාන්යයෙන් උච්චාරණය වනුයේ සැකිල්ල:IPAEng යනුවෙනි. අනෙකුත් ජපන් ප්රකාශකයන් මෙම ප්රහේලිකාව හඳුන්වනුයේ, මුල් එ. ජ. නාමය වන අංක පෙදෙස යනුවෙන් හෝ, කෙටියෙන් "නන්පුරේ"(ナンプレ) ලෙසිනි.[5] සමහරක් ප්රකාශකයන් නාමය වහරන්නේ "සූ දොකු" ලෙසය.
සූදකු ප්රහේලිකාවේ සංඛ්යාංක භාවික වනුයේ හුදෙක් පහසුව සඳහා වේ; සංඛ්යාංක අතර අංකගණිතමය බන්ධුතාවයන් අනාදාල වේ. අකුරු, හැඩ, හෝ වර්ණ වැනි කුමන හෝ ප්රභින්න සංකේත කට්ටලයක් මේ සඳහා සුදුසු වේ. සත්යවශයෙන්ම, ඊඑස්පීඑන් විසින් ප්රකාශිත සූදකු ප්රහේලිකාවන්හි 1 සිට 9 දක්වා සංඛ්යා වෙනුවට බේස්බෝල් පිටියක ස්ථාන ආදේශ කර තිබූ අතර, විස් සඟරාව විසින්, රූපවාහිනී කථා මාලාවේ පළමු ප්රමුඛ නළුවන් නව දෙනා සංඛ්යාංක නවය වෙනුවට යොදා ගනිමින්, ක්රීඩාවේ ඩොක්ට හූ ප්රවාචනයක් ප්රකාශයට පත් කොට තිබුණි. ප්රහේලිකාවේ උත්පාදකයා වන ඩෙල් සඟරා විසින්, 1979 දී වූ පළමු ප්රකාශයේ සිට එහි සඟරාවන්හි අංක පෙදෙස සඳහා සංඛ්යාංක භාවිත කිරීම පුරුද්දක් කොට ගෙන තිබුණි.[5]
මූලෝපායයන්[සංස්කරණය]
ප්රහේලිකාවක් විසඳීමෙහි මූලෝපායය, ක්රියාවලින් ත්රිත්වයක සංකලනයක් ලෙස සැලකේ: පරිලෝකනය, ලකුණු කිරීම, හා විශ්ලේෂණයThe approach to analysis may vary according to the concepts and the representations on which it is based.
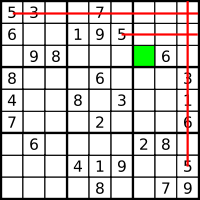
පරිලෝකනය[සංස්කරණය]
පරිලෝකනය කරනු ලබන්නේ විසඳුම ආරම්භයෙහිදී හා අතරතුරදීය. විශ්ලේෂණයන් අතරතුරදී පරිලෝකනයන් සිදුකල යුත්තේ එක් වරක් පමණි. පරිලෝකනය ශිල්පක්රම දෙකකින් සමන්විත වේ:
- හරස්-කඩරේඛනය: මෙය තිරස් පේලි පරිලෝකනය කරමින් හා නොගැලපෙන කොටු බැහැර කිරීමේ ක්රියාවලියක් තුලින් යම් පෙදෙසක හෝ කොටසක කුමන පේලියක් කිසියම් අංකයක් අඩංගු වීමට සුදුසුද යන්න සොයා බැලීමය. මෙම ක්රියාවලිය සිරස් පේළි සඳහාද පුනරාවර්තනය කරනු ලැබේ. 1– 9 දක්වා අංක සියල්ල විමසීමට ලක් කරමින්, මෙම ක්රියාවලිය ක්රමානුකූලව සිදු කිරීම ඉතා වැදගති.
- අන්තර්ගත වී නොමැති අංක හඳුනාගැනීම සඳහා, ප්රදේශයන්හි, තිරස් පේළි, හා සිරස් පේළි වලදී 1–9 ගැන බැලීම. සොයාගත් අවසාන අංකය පදනම් කොට ගෙන මෙම ගැන බැලීම සිදු කිරීම, ගවේෂණය වේගවත් කිරීමට ඉවහල් විය හැක. විශේෂයෙන්, දුෂ්කර ප්රහේලිකාවන්හීදී, සිහි තබා ගත යුතු කරුණක් වනුයේ, යම් කොටුවක් සඳහා නියමිත අංකය නිශ්චය කිරීමේ හොඳම ක්රමය වනුයේ, පසුපසට ගැන බැලීම —එනම්, වියනොහැකි අගයයන් සොයාගැනීමට කොටුවක පෙදෙසල තිරස් පේළිය, හා සිරස් පේළිය පරිලෝකනය කොට, ඉතිරි වන්නේ කුමක් දැයි විමසා බැලීමයි. මෙම ආකාරයට සිදු කිරීමෙන්, කොටුවක් සඳහා විකල්පය එක් ප්රවේශනයක් දක්වා ලඝු කර ගැනීමෙන් සූදකු ක්රීඩාව වචනයේ පරිසමාප්ත අර්ථයෙන්ම සිදුකල හැක.
Advanced solvers look for "contingencies" while scanning, narrowing a numeral's location within a row, column, or region to two or three cells. When those cells lie within the same row and region, they can be used for elimination during cross-hatching and counting. Puzzles solved by scanning alone without requiring the detection of contingencies are classified as "easy"; more difficult puzzles are not readily solved by basic scanning alone.

Marking up[සංස්කරණය]
Scanning stops when no further numerals can be discovered, making it necessary to engage in logical analysis. One method to guide the analysis is to mark candidate numerals in the blank cells.
Subscript notation[සංස්කරණය]
In subscript notation, the candidate numerals are written in subscript in the cells. Because puzzles printed in a newspaper are too small to accommodate more than a few subscript digits of normal handwriting, solvers may create a larger copy of the puzzle. Using two colours, or mixing pencil and pen marks can be helpful.
Dot notation[සංස්කරණය]
The dot notation uses a pattern of dots in each square, where the dot position indicates a number from 1 to 9. The dot notation can be used on the original puzzle. Dexterity is required in placing the dots, since misplaced dots or inadvertent marks lead to confusion and may not be easily erased.
Another technique is to mark the numerals that a cell cannot be. The cell starts empty and as more constraints become known, it slowly fills until only one mark is missing. Assuming no mistakes are made and the marks can be overwritten with the value of a cell, there is no longer a need for any erasures.
විශ්ලේශණය[සංස්කරණය]
The two main approaches to analysis are "candidate elimination"[6] and "what-if".[7]
Candidate elimination[සංස්කරණය]
In "candidate elimination", progress is made by successively eliminating candidate numerals to leave one choice for a given cell. After each answer is found, another scan may be performed—usually checking to see the effect on contingencies. In general, if entering a numeral prevents completion of other empty cells, then the numeral can be eliminated as a candidate.
One method of candidate elimination works by identifying "matched cell groups". For instance, if precisely two cells within a scope (a particular row, column, or region) contain the same two candidate numerals (p,q), or if precisely three cells within a scope contain the same three candidate numerals (p,q,r), these cells are said to be matched. The placement of those candidate numerals anywhere else within the same scope would make a solution impossible, allowing the numbers to be eliminated as candidates from those other cells.
What-if[සංස්කරණය]
In the "what-if" approach (also called "guess-and-check", "bifurcation", "backtracking" and "Ariadne's thread"), a cell with two candidate numerals is selected, and a guess is made. The results are followed until a duplication is found or a cell is left without a candidate, in which case the alternative must have been the solution. For each cell's candidate, the question is posed: 'will entering a particular numeral prevent completion of the other placements of that numeral?' If 'yes', then that candidate can be eliminated. If the "what-if" exercises show that either candidate is possible, then another pair should be tried. Alternatively, if the "what-if" exercises for both candidates imply an identical result, then that result is known. The what-if approach requires a pencil and eraser or a good layout memory.
There are three kind of conflicts, which can appear during puzzle solving:
- basic conflicts - there are only N-1 different candidates in N cell in the area
- fish conflicts - when eliminating number from N rows/columns, it will disappear also from N+1 columns/rows.
- unique conflicts - this pattern means multiple solutions, all numbers in the pattern exist exactly two times in every area, row and column. If there is only one candidate in the cell, any virtual candidate can be added.
Encountering any of those would indicate that the puzzle is not uniquely solvable. Encountering any of them as a consequence of "what-if" indicates that an untried alternative is correct.
Computer solutions[සංස්කරණය]
There are three general approaches taken in the creation of serious Sudoku-solving programs: human solving methods, rapid-style methods, and pure brute-force algorithms. Human-style solvers will typically operate by maintaining a mark-up matrix, and search for contingencies, matched cells, and other elements that a human solver can use to determine and exclude cell values.
Many rapid-style solvers employ backtracking searches, with various pruning techniques in order to help reduce the size of the search tree. The term rapid-style may be misleading: Most human-style solvers run considerably faster than a rapid-style solver, although the latter takes less time to write and is more easily adapted to larger grids. A purely brute-force algorithm is very simple and finds a solution to a puzzle essentially by "counting" upward until a string of eighty-one digits is constructed which satisfies the row, column, and box constraints of the puzzle.
Rapid solvers are preferred for trial-and-error puzzle-creation algorithms, which allow for testing large numbers of partial problems for validity in a short time; human-style solvers can be employed by hand-crafting puzzlesmiths for their ability to rate the difficulty of a created puzzle and show the actual solving process their target audience can be expected to follow.
Although typical Sudoku puzzles (with 9×9 grid and 3×3 regions) can be solved quickly by computer, the generalization to larger grids is known to be NP-complete. Various optimization methods have been proposed for large grids.
Details of computer solutions may be found on the page on the Algorithmics of Sudoku.
Difficulty ratings[සංස්කරණය]
සැකිල්ල:Unreferenced-section The difficulty of a puzzle is based on the relevance and the positioning of the given numbers rather than their quantity. Surprisingly, the number of givens often does not reflect a puzzle's difficulty. Computer solvers can estimate the difficulty for a human to find the solution based on the complexity of the solving techniques required. Some online versions offer several difficulty levels.
Most publications sort their Sudoku puzzles into four or five rating levels, although the cut-off points and the names of the levels vary widely. Typically, the levels are "easy", "intermediate", and "hard". Extremely difficult puzzles are known as "diabolical" or "evil". An easy puzzle can be solved using only scanning; an intermediate puzzle may take markup to solve; a hard puzzle will usually take analysis.
Another approach is to rely on the experience of a group of human test solvers. Puzzles can be published with a median solving time rather than an algorithmically defined difficulty level.
Difficulty is a very complex topic, subject to much debate on the Sudoku forums, because it may depend on the concepts and visual representations one is ready to use.
Construction[සංස්කරණය]
Building a Sudoku puzzle can be performed by predetermining the locations of the givens and assigning them values only as needed to make deductive progress. This technique gives the constructor greater control over the flow of puzzle solving, leading the solver along the same path the compiler used in building the puzzle. Great caution is required, however, as failing to recognize where a number can be logically deduced at any point in construction—regardless of how tortuous that logic may be—can result in an unsolvable puzzle when defining a future given contradicts what has already been built. Building a Sudoku with symmetrical givens is a simple matter of placing the undefined givens in a symmetrical pattern to begin with.
Nikoli Sudoku are hand-constructed, with the author being credited; the givens are always found in a symmetrical pattern.[8] Dell Number Place Challenger (see Variants below) puzzles also list authors. The Sudoku puzzles printed in most UK newspapers are apparently computer-generated but employ symmetrical givens; The Guardian famously claimed that because they were hand-constructed, their puzzles would contain "imperceptible witticisms" that would be very unlikely in computer-generated Sudoku.
විවිධ වර්ග[සංස්කරණය]


Although the 9×9 grid with 3×3 regions is by far the most common, variations abound. Sample puzzles can be 4×4 grids with 2×2 regions; 5×5 grids with pentomino regions have been published under the name Logi-5; the World Puzzle Championship has featured a 6×6 grid with 2×3 regions and a 7×7 grid with six heptomino regions and a disjoint region. Larger grids are also possible. The Times offers a 12×12-grid Dodeka sudoku with 12 regions of 4×3 squares. Dell regularly publishes 16×16 Number Place Challenger puzzles (the 16×16 variant often uses 1 through G rather than the 0 through F used in hexadecimal). Nikoli offers 25×25 Sudoku the Giant behemoths.
Another common variant is to add restrictions on the placement of numbers beyond the usual row, column, and region requirements. Often the restriction takes the form of an extra "dimension"; the most common is to require the numbers in the main diagonals of the grid also to be unique. The aforementioned Number Place Challenger puzzles are all of this variant, as are the Sudoku X puzzles in the Daily Mail, which use 6×6 grids.
A variant named "Mini Sudoku" appears in the American newspaper USA Today, which is played on a 6x6 grid with 3x2 regions. The object is the same as standard Sudoku, but the puzzle only uses the numbers 1 through 6.
Another variant is the combination of Sudoku with Kakuro on a 9 x 9 grid, called Cross Sums Sudoku, in which clues are given in terms of cross sums. The clues can also be given by cryptic alphametics in which each letter represents a single digit from 0 to 9. An excellent example is NUMBER+NUMBER=KAKURO which has a unique solution 186925+186925=373850. Another example is SUDOKU=IS*FUNNY whose solution is 426972=34*12558.
Killer Sudoku combines elements of Sudoku with Kakuro - usually no initial numbers are given, but the 9*9 grid is divided into regions, each with a number that the sum of all numbers in the region must add up to, with no repeated numerals. These must be filled in while obeying the standard rules of Sudoku.
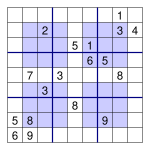
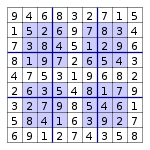
Many newspapers include the popular Hypersudoku such as The Age. The layout is identical to a normal Sudoku, but with additional interior areas defined in which the numbers 1 to 9 must appear. The solving algorithm is slightly different from the normal Sudoku puzzles because of the leverage on the overlapping squares. This overlap gives you more information to logically reduce the possibilities in the remaining squares. The approach to playing is still similar to sudoku but with possibly more emphasis on scanning the squares and overlap rather than columns and rows.
Puzzles constructed from multiple Sudoku grids are common. Five 9×9 grids which overlap at the corner regions in the shape of a quincunx is known in Japan as Gattai 5 (five merged) Sudoku. In The Times, The Age and The Sydney Morning Herald this form of puzzle is known as Samurai SuDoku. The Baltimore Sun publishes a puzzle of this variant (titled High Five) in their sunday edition. Puzzles with twenty or more overlapping grids can be found in some Japanese publications. [තහවුරු කර නොමැත] Often, no givens are to be found in overlapping regions. Sequential grids, as opposed to overlapping, are also published, with values in specific locations in grids needing to be transferred to others.
Alphabetical variations have emerged; there is no functional difference in the puzzle unless the letters spell something. Some variants, such as in the TV Guide, include a word reading along a main diagonal, row, or column once solved; determining the word in advance can be viewed as a solving aid. A more loose variant on the sudoku concept is seen in Squaro, wherein circles at the vertices of a grid are filled in to meet the requirements of numbers in that grid in a combination of sudoku and minesweeper.
A tabletop version of Sudoku can be played with a standard 81-card Set deck (see Set game). A three-dimensional Sudoku puzzle was invented by Dion Church and published in the Daily Telegraph in May 2005. There is a Sudoku version of the Rubik's Cube named Sudokube.
The 2005 U.S. Puzzle Championship included a variant called Digital Number Place: rather than givens, most cells contain a partial given—a segment of a number, with the numbers drawn as if part of a seven-segment display. This version has also appeared in GAMES magazine.
සූදකු තුල ගණිතය[සංස්කරණය]
- මූලික ලිපිය: සූදකු තුල ගණිතය
A completed Sudoku grid is a special type of Latin square with the additional property of no repeated values in any partition of the 9×9 block into contiguous 3×3 blocks. The relationship between the two theories is now completely known, after Denis Berthier has proven in his recent book, "The Hidden Logic of Sudoku", that a first order formula that does not mention blocks (also called boxes or regions) is valid for Sudoku if and only if it is valid for Latin Squares (this property is trivially true for the axioms and it can be extended to any formula).
The first known calculation of the number of classic 9×9 Sudoku solution grids was posted on a USENET newsgroup rec.puzzles in September of 2003[9] and is 6,670,903,752,021,072,936,960 (OEIS හි A107739 අනුක්රමය). This is roughly 0.00012% the number of 9×9 Latin squares. A detailed calculation of this figure was provided by Bertram Felgenhauer and Frazer Jarvis in 2005[10]. Various other grid sizes have also been enumerated—see the main article for details. The number of essentially different solutions, when symmetries such as rotation, reflection and relabelling are taken into account, was shown by Ed Russell and Frazer Jarvis to be just 5,472,730,538[11] (OEIS හි A109741 අනුක්රමය).
The maximum number of givens provided while still not rendering a unique solution is four short of a full grid; if two instances of two numbers each are missing and the cells they are to occupy form the corners of an orthogonal rectangle, and exactly two of these cells are within one region, there are two ways the numbers can be assigned. Since this applies to Latin squares in general, most variants of Sudoku have the same maximum. The inverse problem—the fewest givens that render a solution unique—is unsolved, although the lowest number yet found for the standard variation without a symmetry constraint is 17, a number of which have been found by Japanese puzzle enthusiasts,[12][13] and 18 with the givens in rotationally symmetric cells. Over 47,000 examples of Sudokus with 17 givens resulting in a unique solution are known.
History[සංස්කරණය]

Number puzzles first appeared in newspapers in the late 19th century, when French puzzle setters began experimenting with removing numbers from magic squares. Le Siècle, a Paris-based daily, published a partially completed 9×9 magic square with 3×3 sub-squares in 1892.[14] It was not a Sudoku because it contained double-digit numbers and required arithmetic rather than logic to solve, but it shared key characteristics: each row, column and sub-square added up to the same number.
Within three years Le Siècle's rival, La France, refined the puzzle so that it was almost a modern Sudoku. It simplified the 9×9 magic square puzzle so that each row and column contained only the numbers 1–9, but did not mark the sub-squares. Although they are unmarked, each 3×3 sub-square does indeed comprise the numbers 1–9. However, the puzzle cannot be considered the first Sudoku because, under modern rules, it has two solutions. The puzzle setter ensured a unique solution by requiring 1–9 to appear in both diagonals.
These weekly puzzles were a feature of newspaper titles including L'Echo de Paris for about a decade but disappeared about the time of the First World War.[15]
According to Will Shortz, the modern Sudoku was most likely designed anonymously by Howard Garns, a 74-year-old retired architect and freelance puzzle constructor from Indiana, and first published in 1979 by Dell Magazines as Number Place (the earliest known examples of modern Sudoku). Garns's name was always present on the list of contributors in issues of Dell Pencil Puzzles and Word Games that included Number Place, and was always absent from issues that did not.[5] He died in 1989 before getting a chance to see his creation as a worldwide phenomenon.[5] It is unclear if Garns was familiar with any of the French newspapers listed above.
The puzzle was introduced in Japan by Nikoli in the paper Monthly Nikolist in April 1984[5] as Suuji wa dokushin ni kagiru (数字は独身に限る), which can be translated as "the digits must be single" or "the digits are limited to one occurrence." At a later date, the name was abbreviated to Sudoku by Maki Kaji (鍜治 真起, Kaji Maki), taking only the first kanji of compound words to form a shorter version.[5] In 1986, Nikoli introduced two innovations: the number of givens was restricted to no more than 32, and puzzles became "symmetrical" (meaning the givens were distributed in rotationally symmetric cells).උපුටාදැක්වීම් දෝෂය: <ref> ටැගය සොයාගත නොහැකි බැවින් </ref> වසා දමමින් Knowing that British newspapers have a long history of publishing crosswords and other puzzles, he promoted Sudoku to The Times in Britain, which launched it on 12 November 2004 (calling it Su Doku).
The rapid rise of Sudoku in Britain from relative obscurity to a front-page feature in national newspapers attracted commentary in the media and parody (such as when The Guardian's G2 section advertised itself as the first newspaper supplement with a Sudoku grid on every page[16]). Recognizing the different psychological appeals of easy and difficult puzzles, The Times introduced both side by side on 20 June 2005. From July 2005, Channel 4 included a daily Sudoku game in their Teletext service. On 2 August, the BBC's programme guide Radio Times featured a weekly Super Sudoku.
Even the Greeks owe the publication of their first Sudoku magazine to British influence. It was at Heathrow airport in the summer of 2005 that a Greek computer magazine publisher first laid eyes on a British Sudoku magazine and - realizing the opportunity - proceeded to purchase the necessary software and quickly launch the first local Sudoku magazine that became an instant success.
In the United States, the first newspaper to publish a Sudoku puzzle by Wayne Gould was The Conway Daily Sun (New Hampshire), in 2004.[17]
The world's first live TV Sudoku show, Sudoku Live, was a puzzle contest first broadcast on 1 July 2005 on Sky One. It was presented by Carol Vorderman. Nine teams of nine players (with one celebrity in each team) representing geographical regions competed to solve a puzzle. Each player had a hand-held device for entering numbers corresponding to answers for four cells. Phil Kollin of Winchelsea, England was the series grand prize winner taking home over £23,000 over a series of games. The audience at home was in a separate interactive competition, which was won by Hannah Withey of Cheshire.
Later in 2005, the BBC launched SUDO-Q, a game show that combines Sudoku with general knowledge. However, it uses only 4x4 and 6x6 puzzles.
Sudoku software is now also very popular on PCs, websites, and mobile phones. It comes with many distributions of Linux. It has also been released on portable video game handhelds such as the Nintendo DS, PlayStation Portable, the Game Boy Advance, and even on several iPod models. One of the most popular video games featuring Sudoku is Brain Age: Train Your Brain in Minutes a Day!. Critically and commercially well received, it generated particular praise for its Sudoku implementation[1] සංරක්ෂණය කළ පිටපත 2008-05-09 at the Wayback Machine[2][3] and sold more than 8 million copies worldwide.[4] Due to its popularity, Nintendo made a second Brain Age game titled Brain Age2, which has over 100 new sudoku puzzles and other activities.
තරඟ[සංස්කරණය]
- පලමු ලෝක සුදෝකු ශුරතාවය ඉතාලියේ Luccaහිදි 2006 මාර්තු මස 10 දින 12 දින තෙක් පැවැත්වින. ජයාග්රාහිකාව වුයේ Czech ජනරජයේ Jana Tylova.[18] තරගයට විවිධ වර්ගයේ සුදොකු ප්රෙහෙලිකාවන් ඇතුලත්ව තිබිනි.[19]
- දෙවන ලෝක සුදෝකු ශුරතාවය Prague 2007 මාර්තු 28 සිට අප්රේල් 1 තෙක් පැවැත්වින. [20] කේවල තරගයෙන් ඇමරිකාවේ Thomas Snyder කන්ඩායම් තරගයෙන් ජපානය ද ජය ගන්නා ලදි.[21]
- Hosted by renowned puzzle master Will Shortz, The Philadelphia Inquirer Sudoku National Championship was the first U.S. Sudoku Championship. Thomas Snyder was the winner of the expert division, receiving $10,000 and a spot on the U.S. National Sudoku Team at the 2008 World Sudoku Championship in India.[22]
- The third World Sudoku Championship was held in Goa, India from April 14-16, 2008. Thomas Synder repeated as the individual overall championship, and also won the first ever Classic Trophy (a subset of the competition counting only classic Sudoku). The Czech Republic won the team competition.[23]
See also[සංස්කරණය]
- Mathematics of Sudoku
- Algorithmics of Sudoku
- List of Sudoku terms and jargon
- Killer sudoku
- Sudokube (3D variant)
- Latin square
- Logic puzzle
- List of Nikoli puzzle types
- Kakuro
- Nonogram (aka Paint by numbers, O'ekaki)
- Futoshiki
- KenKen
ආශ්රිත[සංස්කරණය]
- ↑ ලියොනාඩ් ඉයුලර්. මායා කොටු පිළිබඳ.
- ↑ සූදකු ප්රභේදන.
- ↑ බ්රයන් හේස් (2006). අන්වෙඩ් නම්බර්ස් (අවිවාහක අංක). Vol. 94. ඇමරිකන් සයන්ටිස්ට්. pp. 12–15.
- ↑ 4.0 4.1 History of Sudoku in our site.
- ↑ 5.0 5.1 5.2 5.3 5.4 5.5 Ed Pegg Jr.'s Math Games: Sudoku Variations.
- ↑ "Goals of Sukoku-Grok". 2005.
{{cite web}}: Unknown parameter|accessmonth=ignored (|access-date=suggested) (help); Unknown parameter|accessyear=ignored (|access-date=suggested) (help) - ↑ "Play Sudoku". Online Learning Haven.
{{cite web}}: Unknown parameter|accessmonthday=ignored (help); Unknown parameter|accessyear=ignored (|access-date=suggested) (help) - ↑ "Rules and history of Sudoku from Nikoli".
- ↑ "Combinatorial question on 9x9". Google newsgroups archive.
{{cite web}}: Unknown parameter|accessmonthday=ignored (help); Unknown parameter|accessyear=ignored (|access-date=suggested) (help) - ↑ Jarvis, Frazer (2006-07-31). "Sudoku enumeration problems". Frazer Jarvis's home page.
{{cite web}}: Unknown parameter|accessmonthday=ignored (help); Unknown parameter|accessyear=ignored (|access-date=suggested) (help) - ↑ Jarvis, Frazer (2005-09-07). "There are 5472730538 essentially different Sudoku grids ... and the Sudoku symmetry group". Frazer Jarvis's home page.
{{cite web}}: Unknown parameter|accessmonthday=ignored (help); Unknown parameter|accessyear=ignored (|access-date=suggested) (help); Unknown parameter|coauthors=ignored (|author=suggested) (help) - ↑ "プログラミングパズルに関心のある人は雑談しましょう". プログラミングパズル雑談コーナー / Programming Puzzle Idle Talk Corner (Japanese බසින්).
{{cite web}}: Unknown parameter|accessmonthday=ignored (help); Unknown parameter|accessyear=ignored (|access-date=suggested) (help)CS1 maint: unrecognized language (link) - ↑ Royle, Gordon. "Minimum Sudoku".
{{cite web}}: Unknown parameter|accessmonthday=ignored (help); Unknown parameter|accessyear=ignored (|access-date=suggested) (help) - ↑ Boyer, Christian (2006). "Supplément de l'article « Les ancêtres français du sudoku »" (PDF). Pour la Science: 1–6. සම්ප්රවේශය 2006-09-16.
{{cite journal}}: Unknown parameter|month=ignored (help) - ↑ Malvern, Jack (2006-06-03). "Les fiendish French beat us to Su Doku". Times Online. සම්ප්රවේශය 2006-09-16.
- ↑ "G2, home of the discerning Sudoku addict". The Guardian. Guardian Newspapers Limited. 2005-05-13. සම්ප්රවේශය 2006-09-16.
- ↑ New York Times corrections column, April 2, 2007, p. A2
- ↑ "Sudoku title for Czech accountant" (Free). BBC NEWS. 2006-03-11. සම්ප්රවේශය 2006-09-11.
- ↑ "World Sudoku Championship 2006 Instructions Booklet" (PDF).
- ↑ "Report on the 8th General Assembly of the World Puzzle Federation". WPF. 2006-10-30. 2007-09-26 දින මුල් පිටපත (Free) වෙතින් සංරක්ෂණය කරන ලදී. සම්ප්රවේශය 2006-11-15.
- ↑ "Thomas Snyder wins World Sudoku Championship". US Puzzle Team. 2007-03-31. 2008-04-13 දින මුල් පිටපත වෙතින් සංරක්ෂණය කරන ලදී. සම්ප්රවේශය 2008-04-18.
- ↑ "Thomas Snyder, World Sudoku champion" (Free). Philadelphia Inquirer. 2007-10-21. සම්ප්රවේශය 2007-10-21.
- ↑ "It's a puzzle but sun, sea and beer can't compete with Sudoku for British team". TimesOnline. 2008-04-17. සම්ප්රවේශය 2008-04-18.
External links[සංස්කරණය]
- Sudoku at the Open Directory Project – An active listing of Sudoku links.
- Father of Sudoku puzzles next move BBC
