කාච
මෙම ලිපිය වනාහි Lens (optics) ලිපියෙහි ඉංග්රීසි භාෂාවේ සිට සිංහල වෙත නොනිමි පරිවර්තනයකි . ඉංග්රීසි සහ සිංහල යන භාෂාවන්හි සුදුසු හා ප්රමාණවත් පරිචයක් ඇත්නම්, මෙම පරිවර්තනය සම්පූර්ණ කිරීමට ඔබට අවකාශ ඇත. අදාල විෂය පිලිබඳ දැනුවත්නම්, නැවුම් ස්වයං නිර්මාණයක් ලෙස ලිපිය සම්පූර්ණ කිරීමට ඔබට අවකාශ ඇත. |
මෙම ලිපිය වැඩිදියුණු කළයුතුව ඇත. ඔබ මෙම මාතෘකාව පිලිබඳව දැනුවත්නම්, නව කරුණු එක්කිරීමට දායකවන්න. |


කාචයක් යනු ඉතා නිවැරදි සමමිතික අක්ෂයක් ඇති ආලෝකය එතුලින් ගමන් කරන සහ වර්තනය කරමින් අභිසරණය හෝ අපසරණය කරන ප්රකාශ උපකරණයකි.[citation needed] සරල කාචයක් තනි ප්රකාශ උපකරණයකින් සමන්විත වේ. සංයුක්ත කාචයක් යනු සරල කාච ගණනාවක් එකම අක්ෂයක් ඔස්සේ තැබීමෙන් සෑදුනු උපකරණයකි. කාච කිහිපයක් භාවිතා කිරීමෙන් ප්රකාශ අපේරණය අඩුකරගැනීමට හැකි වේ. කාච සාමාන්යයෙන් වීදුරු හෝ විනිවිද පෙනෙන ප්ලාස්ටික් වලින් තනනු ලැබේ. විද්යුත් චුම්භක තරංග වර්තනය කිරීමට හැකි උපකරණද කාච යනුවෙන් හැඳින්වේ. උදාහරණ වශයෙන් පැරෆින් ඉටි වලට ක්ෂුද්ර තරංග වර්තනය කළ හැක.
ඉතිහාසය[සංස්කරණය]


පැරණිතම කාච මෙවලම පිළිබඳ සඳහන් වනුයේ ක්රි.පු. 640 දීය. නිනිවෙහ් හි කැණීම්වලින් සොයා ගැණුනු ආකර ස්ඵටික කාචයක් පිළිබදවය. ඉපැරණි ග්රීසියේ දාහක කාචයක් ගැන සඳහන් කරමින් (හිරු කිරණ නාභිගත කරමින් ගින්දර නිපදවීමට භාවිතා කළ ද්වි උත්තල කාචයක් ඇරිස්ටෝෆේන් විසින් රචිත වළාකුළු (ක්රි.පු 424) නම් නාට්ය මුලින්ම කාච පිළිබඳ ලියූ වාර්තාවයි. ශෝධක කාචවල විය හැකි පළමු භාවිතය ගැන සදහන් කරමින් ප්ලයිනි (23 – 79) විසින් ඔහුගේ වාර්තාවක රෝමාණු අධිරාජ්යයා ද දාහක කාච පිලිබදව දත් බව පවසා සිටී. නීරෝ මාණික්යයක් භාවිතයෙන් (අනුමාන වශයෙන් අවිදුර දෘෂ්ටිකත්වය නිවැරදි කිරීමට අවතල කාචයක්) කඩු හරඹ ක්රීඩා නැරඹීය. ප්ලයින් හා සෙනෙකා (ක්රිපු. 3 – 65) ජලය පිරි වීදුරු ගෝලයක විශාලක හැකියාව විස්තර කරයි.
Lens (කාචය) යන නම Lentil නම් ලතින් නමින් පැමිණි ඇත. මක් නිසාද යත් ද්වි උත්තල කාචයක් Lentil හැඩතිය. භෝගවල ගණය Lens වන අතර බහුලව ආහාරයට ගන්නා ප්රභේදයක් නිසා Lens Culinaris නම් දී ඇත. ජ්යාමිතික හැඩතලයකට ද මෙම ශාකයේ නම ඇසුරින් නම් යෙදීම කර ඇත.
අරාබි ගණිතඥ ඉබන් සාහිල් (ක්රි.ව. 940 – 1000) දැනට දන්නා ස්නේලිගේ නියමය කාචවල හැඩය ගණනය කිරීමට භාවිතා කර ඇත. ඉබන් අල් හයිතම් (965 – 1038) මිනිස් ඇසේ ඇති කාච දෘෂ්ටි විතානය මත ප්රතිබිම්භයක් සාදන්නේ කෙසේ දැයි විස්තර කරමින් “The Book of Optics” නමින් ප්රථම ප්රධාන ප්රකාශ ග්රන්ථය ලිවීය.
1999 වසරේ දී ස්වීඩනයේ ගොට්ලන්ඩ් හි ෆ්රොජෙල් ආශ්රිතව පිහිටි වයිකිංවරුන්ට අයත් වරාය ආශ්රිතව නඟරයේ කරන ලද කැනීම්වලින් පළිඟු පාෂාණ ඇසුරින් නිර්මාණය කළ විස්බි කාච හමුවිය. මේවා ෆ්රොජෙල්හි දී ලී දඬු මත කරකැවීම කාච සකස් කිරීම සිදු කළ වැඩ පළවල් තුළ රිටිලේයත් භාවිතයෙන් 11 වන සහ 12 වන සියවස් තුළ දී නිර්මාණය කළ ඒවා වේ. මේවායේ ප්රමිතිය 1950 දශකයේ නිර්මාණය කළ ගෝලීය කාචවල ප්රමිතියේ තරමටම උසස් වේ. වයිකිංවරුන්ගේ කාච මඟින් ගිනි දැල්වීමට ප්රමාණවත් තරම් සූර්යාලෝකය නාභිගත කිරීම කළ හැකි විය.
අප අනුමාන කරන අන්දමට 1280 ඉතාලියේදී ඇස් කණ්ණාඩි සොයා ගැනීම හා 11 වන ශත වර්ෂයේ කියවුම් ගල්වල භාවිතය තෙක් කාචවල භාවිතය පුළුල්ව විහිදීම සිදු නොවිණි. කුසාහි නිකොලස් 1451 දී අවිදුර දෘෂ්ටිකත්වයේ ප්රතිකාර සදහා අවතල කාචවල ප්රයෝජන සොයා ගත් ප්රථමයා ලෙස පිළිගනී.
අබේගේ සයින් නියතය (අර්නස්ට් අබේ (1860) සිහි වීම සඳහා මෙසේ නම් කර ඇත) අක්ෂය මත මෙන්ම අක්ෂයෙන් පිටත වස්තුවල තියුණු ප්රතිබිම්භයක් ලබා ගැනීමට කාච හෝ වෙනත් ප්රකාශ පද්ධතියක් ඉටු කළ යුතු අවශ්යතාවයකි. සයින අවශ්යතාව අන්වීක්ෂ වැනි ප්රකාශ උපකරණවල නිර්මාණය මෙමඟින් විප්ලවීකරණය කළ අතර ප්රකාශ උපකරණවල ප්රමුඛ සැපයුම්කරුවෙකු ලෙස කාල් සෙයිස් සමාගම පිහිටුවීමට අනුබලයක් විය.
සරල කාච නිර්මාණය[සංස්කරණය]
බොහෝ කාච ගෝලීය කාච වේ: කාච අක්ෂය එහි පෘෂ්ඨ දෙකටම ලම්භක වන අතර පෘෂ්ඨ ගෝල පෘෂ්ඨ වල කොටස් වේ. එම එක් එක් පෘෂ්ඨයන් අශිසාරී (පිම්බුනු ආකරයේ), අපසාරී (හැකිලුනු ආකාරයේ) හෝ තල පෘෂ්ඨ විය හැකිය. ගෝල දෙකෙහි කේන්ද්ර යාකරන රේඛාව කාචයේ අක්ෂය වේ. කාච නිෂ්පාදනය කරන ආකාරය අනුව සාමාන්යයෙන් කාච අක්ෂය කාචයේ මධ්ය හරහා ගමන්කරයි. සමහර විට කාචය නිෂ්පාදනය කිරීමෙන් අනතුරුව කාචයේ හැඩය වෙනස් කිරීම් වලට භාජනය කරනු ලබයි. එවිට කාචයේ මධ්ය හරහා එහි අක්ෂය ගමන් නොකරනු ඇති.
 |
 |
ටෝරික් (Toric) හෙවත් ගෝලීය-සිලින්ඩරාකාර කාච වල පෘෂ්ඨ දෙකෙහි වක්රතා අරයන් එකිනෙකට වෙනස්වේ එමෙන්ම ඒවා එකම තලයක පිහිටන්නේද නැත. එවිට ඒවායේ විශාලන බලය විවිධ ස්ථාන වලදී විවිධ අගයන් ගනී.
ගෝලීය නොවන කාච මීට වඩා සංකීර්ණ බවක් ගනී. මෙම කාචවල එක් පෘෂ්ඨයක් හෝ පෘෂ්ඨ දෙකම ගෝලීය හෝ සිලින්ඩරාකාර නොවන හැඩයක් ගනී. මෙම කාච වලින් ප්රකාශ අපේරණය නම් සංසිද්ධිය අවම කරගත හැකිය.
සරල කාච වර්ග[සංස්කරණය]
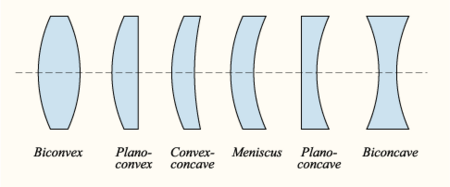
කාච දෘෂ්ටි පෘෂ්ඨයේ වක්රතාව අනුව වර්ගීකරණය කර ඇත. පෘෂ්ඨ දෙකම උත්තල නම් කාචයක් ද්වි උත්තල (ද්වි-උත්තල හෝ උත්තල පමණක්) වේ. අවතල පෘෂ්ඨ දෙකක් සහිතව කාච ද්වි අවතල (හෝ අවතල පමණක්) වේ. පෘෂ්ඨවලින් එකක් පැතලි නම් අනෙක් පෘෂ්ඨයේ වක්රතාවය මත තල උත්තල හෝ තල අවතල වේ. උත්තල පැත්තක් හා අවතල පැත්තක් සහිතව කාච උත්තල අවතල හෝ මාවක නම් වේ. මෙම වර්ගයේ කාච ශෝධක කාචවල බහුලව භාවිතා කරයි.
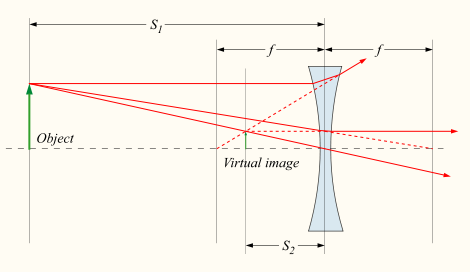
කාචය ද්වි උත්තල හෝ තල උත්තල නම් කාච අක්ෂයට සමාන්තරව සමාන්තර කළ හෝ සමාන්තර ගත ආලෝක කදම්භයක් කාචය හරහා ගමන් කරන විට එය අක්ෂයේ කාචය පිටුපසින් කිසියම් දුරකින් වූ ස්ථානයක් මතට අභිසාරි (හෝ නාභිගත) වේ. (එම දුර නාභිය දුර වේ.) මෙහිදී කාචය ධන හෝ අභිසාරි කාච නම් වේ.
 |
 |
කාචය ද්වි අවතල හෝ තල අවතල නම්, සමාන්තර ගත කළ ආලෝක කදම්භයක් කාචය තුළින් යාමේදී අපසාරී (විහිදී යාම්) වේ. එසේ කාචය සෘණ හෝ අපසාරීකාච නම් වේ. කාචය තුළින් යාමෙන් පසු කදම්භ කාචයට ඉදිරියේ විශේෂ ස්ථානයකින් නිකුත් වෙනවා සේ පෙනීයයි. මෙම ස්ථානයේ සිට කාචයට ඇති දුර නාභිය සේ හදුන්වයි. එසේ නමුත් එය අභිසාරී කාචවල නාභිය දුර ආකාරය හා ප්රතිවිරුද්ධ වේ. / සෘණ වේ.
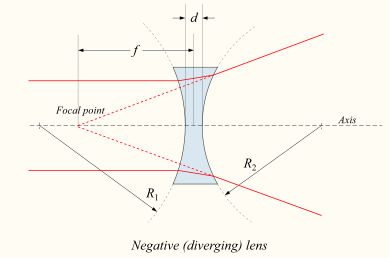 |
 |
උත්තල- අවතල (මාවක) කාච මුහුණත් දෙකෙහි සාපේක්ෂ වක්රතාවය මත ධන හෝ සෘණ වීමට පුළුවන. සෘණ මාවක කාචයක් තියුණු අවතල මුහුණතක් හා පර්යන්තයට වඩා මධ්යයයේ දී සිහින්ය. අනෙක් අතට ධන මාවක කාචයක තියුණු උත්තල මුහුණතක් හා පර්යන්තයට වඩා මධ්යයේදී ඝන වේ. වක්රතාවය සමාන මුහුණත් දෙකක් ඇති පරිපුර්ණ කාචයක ප්රකාශ බලය ශුන්යය. එනම් ආලෝකය අභිසාරී හෝ අපසාරී නොවේ. සැබෑ කාචවල ශුන්ය නොවූ ඝනකමකි, කෙසේ හෝ ප්රකාශ බලය කෙරෙහි බලපායි. නිසැකවම ශූන්ය ප්රකාශ බලය ලබා ගැනීමට මාවක කාචයක කාච ඝනකමට ගණනයට බලපෑම් කළ හැකි යන්තම් අසමාන වක්රතාවයන් තිබිය යුතුය.
ලෙන්ස්මේකර් සමීකරණය[සංස්කරණය]
ලෙන්ස්මේකර්ගේ සමීකරණයෙන් වාතයේදී කාචයක නාභීය දුර ගණනය කළ හැක.
එහි
- යනු කාචයේ නාභීය දුරයි,
- යනු කාචයේ වර්තන අංකයයි,
- යනු ආලෝක ප්රභවයට ආසන්නතම මුහුණතේ වක්රතා අරයයි,
- යනු ආලෝක ප්රභවයට දුරින්ම වූ මුහුණතේ වක්රතා අරයයි, and
- යනු කාචයේ ඝනකමය එනම් සිරස් මුහුණත් 2ක් අතර කාච ඔස්සේ විස්ථාපනය යි
R1 හා R2 කාච අරයයන් සඳහා ලකුණු සම්මුතිය[සංස්කරණය]
වක්රතා අරයයන්ගේ ලකුණු මගින් අනුරූප මුහුණත් උත්තල ද අවතල ද යන්න පෙන්වා දෙයි. ලකුණු සම්මුතිය මෙම වෙනස්වීම් නියෝජනය කිරීමට භාවිතා කළ නමුත් මෙම වගන්තිය මගින් R1 ධන නම් පළමු මුහුණත උත්තල ද R1 ඍණ නම් මුහුණත අවතල ද වේ. පසු මුහුණතට මෙම ලකුණු මාරු වේ. R2 ඍණ නම් මුහුණත උත්තල වේ. දෙකින් කුමන එකෙහි අරය අනන්තය නම් අනුරූප මුහුණත පැතලිය.
සිහින් කාච සමීකරණය[සංස්කරණය]
R1 හා R2 හා සැසඳීමේදී d කුඩා නම් එවිට සන්නිකර්ෂණය යෙදිය හැක. වාතයේ පවතින කාචයක f
මගින් ලබා දේ.
නාභීය දුර f අභිසරණ කාච සඳහා ධන වන අතර අපසාරී කාච ඍණ වේ. 1/f හි අගය ධන වන අතර අපසාරී කාච ඍණ වේ. 1/f හි අගය මීටර්වල ප්රතිලෝමයේ ඒකකවලට සමාන වූ ඩයොප්ටර්වලින් මනින ලද “ප්රකාශ බලය” සේ හැඳින්වේ.
කාච සඳහා ආලෝකය පිටුපස සිට ඉදිරියට සේ හා ආලෝකය ඉදිරියේ සිට පිටුපසට ගමන් කරනා විට එකම නාභීය දුර පවතී. අප්රේරණය වැනි අනෙකුත් ගුණ දිශාවන් දෙකටම එකම අවශ්ය නොවේ.
Imaging properties[සංස්කරණය]

As mentioned above, a positive or converging lens in air will focus a collimated beam travelling along the lens axis to a spot (known as the focal point) at a distance f from the lens. Conversely, a point source of light placed at the focal point will be converted into a collimated beam by the lens. These two cases are examples of image formation in lenses. In the former case, an object at an infinite distance (as represented by a collimated beam of waves) is focused to an image at the focal point of the lens. In the latter, an object at the focal length distance from the lens is imaged at infinity. The plane perpendicular to the lens axis situated at a distance f from the lens is called the focal plane.
If the distances from the object to the lens and from the lens to the image are S1 and S2 respectively, for a lens of negligible thickness, in air, the distances are related by the thin lens formula
- .
This can also be put into the "Newtonian" form:
where and .
What this means is that, if an object is placed at a distance S1 along the axis in front of a positive lens of focal length f, a screen placed at a distance S2 behind the lens will have a sharp image of the object projected onto it, as long as S1 > f (if the lens-to-screen distance S2 is varied slightly, the image will become less sharp). This is the principle behind photography and the human eye. The image in this case is known as a real image.
Note that if S1 < f, S2 becomes negative, the image is apparently positioned on the same side of the lens as the object. Although this kind of image, known as a virtual image, cannot be projected on a screen, an observer looking through the lens will see the image in its apparent calculated position. A magnifying glass creates this kind of image.
The magnification of the lens is given by:
- ,
where M is the magnification factor; if |M|>1, the image is larger than the object. Notice the sign convention here shows that, if M is negative, as it is for real images, the image is upside-down with respect to the object. For virtual images, M is positive and the image is upright.
In the special case that S1 = ∞, then S2 = f and M = −f / ∞ = 0. This corresponds to a collimated beam being focused to a single spot at the focal point. The size of the image in this case is not actually zero, since diffraction effects place a lower limit on the size of the image (see Rayleigh criterion).
The formulas above may also be used for negative (diverging) lens by using a negative focal length (f), but for these lenses only virtual images can be formed.
For the case of lenses that are not thin, or for more complicated multi-lens optical systems, the same formulas can be used, but S1 and S2 are interpreted differently. If the system is in air or vacuum, S1 and S2 are measured from the front and rear principal planes of the system, respectively. Imaging in media with an index of refraction greater than 1 is more complicated, and is beyond the scope of this article.
කාචවල මූර්තන ගුණ[සංස්කරණය]
ඉහත සහඳන් කළ පරිදි වාතය තුළ ඇති ධන එනම්, අභිසාරී කාචයක්, කාච අක්ෂය දිගේ සමාන්තරගතව ගමන් කරන කදම්භයක් කාචයේ සිට f දුරකින් වූ ස්ථානයකට (නාභි ලක්ෂ්යය) වෙත නාභිගත කරයි. විලෝමව , ලක්ෂාකාර ආලෝක ප්රභවයක් නාභි ලක්ෂ්යයේ ස්ථානගත කළ විට ඉන් නිකුත්වන ආලෝකය කාචය මගින් සමාන්තරගත කළ කදම්භයක් බවට හැරවේ. මෙම සිද්ධි 2 කාචවල ප්රතිබිම්භ ආකාරයට උදාහරණ වේ. ඉහත සිද්ධියේදී අනන්ත දුරින්වූ වස්තුවක් (සමාන්තරගත තරංග කදම්භය නියෝජනය කරයි) නාභි ලක්ෂ්යයේ වූ ප්රතිබිම්භයකට නාභි ගත කරයි. ඉන්පසුව නාභි දුරෙහි වූ වස්තුවක් කාචය මගින් අනන්තයේ ප්රතිබිම්භයක් සාදයි. කාචයේ සිට f දුරකින් කාච අක්ෂයට ලම්භකව සිට වූ තලය නාභීය තලය නම් වේ.
පිළිවෙලින් වස්තුවේ සිට කාචයට හා කාචයේ සිට ප්රතිබිම්භයට දුරවල් පිළිවෙලින් S1 , S2 නම් ද එය වාතය තුළ ඇති නොසැලකිය හැකි ඝනකමක් සහිත කාචයක් නම් ද එම දුරවල් අතර සම්බන්ධය පහත සමීකරණයෙන් දක්වයි.
මෙහි අදහස නම් ධන කාචයක ඉදිරියෙන් අක්ෂය දිගේ S1 දුරකින් වස්තුවක් තබා ඇති විට කාචයට පිටුපසින් S2 දුරකින් තිරයක් තබා ඇති විට S1 > f වන පරිදි වෙනස් කරන විට (කාචයේ සිට තිරයට S2 දුර යන්තමින් වෙනස් කරන විට ප්රතිබිම්භය තියුණු බවින් අඩුවේ.) තිරය මත තියුණු ප්රතිබිම්භයක් සෑදේ. මෙය ඡායාරූපකරණයේ මූලධර්මයයි. මෙම සිද්ධියේදී ප්රතිබිම්භය තාත්වික ප්රතිබිම්භයකි. ( එනම් තිරයකට ගත හැකි)
S1 < f වුවහොත් S2 ඍණ වේ. ප්රතිබිම්භය කාචයේ වස්තුව ඇති පැත්තේම වස්තුව මෙන් පෙනෙන පරිදි ස්ථානගත වේ. මෙවැනි වර්ගයේ ප්රතිබිම්භයක් අතාත්වික ප්රතිබිම්භයක් නම් වේ. තිරයක් මත ප්රක්ෂේපණය කළ නොහැක. නිරීක්ෂකයා කාචය තුළින් බැලීමේදී ප්රතිබිම්භය දෘශ්යමාන වේ යැයි ගණනය කළ ස්ථානයේ දක්නට ලැබේ. විශාලක කණ්ණාඩි මෙවැනි ප්රතිබිම්භ තනයි.
කාචවල විශාලනය
මගින් දෙනු ලබයි. M යනු විශාලනයයි. | M| >1 නම් ප්රතිබිම්භය වස්තුවට වඩා විශාලය. ලකුණු සම්මුතිය පෙන්වන පරිදි (M) ඍණ නම් තාත්වික ප්රතිබිම්භය සදහා ප්රතිබිම්භ වස්තුව හා සලකා බැලීමේදී යටිකුරුය. අතාත්වික ප්රතිබිම්භය සදහා M ධන වන අතර ප්රතිබිම්භය උඩුකුරුය.
විශේෂ සිද්ධියක් ලෙස S1 = ¥ හා S2 = f විට M = -f / ¥ = 0 මෙය නාභි ලක්ෂ්යයේ එක් ස්ථානයක් වෙත නාභිගත වූ සමාන්තරගත කළ කදම්භයකට අනුරූප වේ. මෙම සිද්ධියේදී විවර්තන බලපෑම් ප්රතිබිම්භයේ ප්රමාණය පහළ සීමාවක තබන බැවින් එය ඉහත සූත්රයේ දක්වන පරිදි ශූන්යය නොවේ.
ඉහත සූත්ර ඍණ (අපසාරී) කාච සදහා ඍණ නාභි දුරක (f ) භාවිතයෙන් ලබාගත හැකි නමුත් මෙම කාච සදහා අතාත්වික ප්රතිබිම්භ පමණක් සාදයි.
සිහින් නොවන කාච අවස්ථාවන් හෝ වඩා සංකීර්ණ බහු කාච ප්රකාශ පද්ධති සදහා එකම සූත්රය භාවිතා කළ හැකි නමුත් S1 හා S2 පිළිවෙලින් පද්ධතියේ ප්රධාන තලවලට ඉදිරියෙන් හා පිටුපසින් මනියි. මාධ්ය තුළ වර්තන දර්ශකය 1ට වඩා වැඩි විට විශ්ලේෂණය වඩාත් සංකීර්ණ වෙයි.
Aberrations[සංස්කරණය]
Lenses do not form perfect images, and there is always some degree of distortion or aberration introduced by the lens which causes the image to be an imperfect replica of the object. Careful design of the lens system for a particular application ensures that the aberration is minimized. There are several different types of aberration which can affect image quality.
Spherical aberration[සංස්කරණය]
Spherical aberration occurs because spherical surfaces are not the ideal shape with which to make a lens, but they are by far the simplest shape to which glass can be ground and polished and so are often used. Spherical aberration causes beams parallel to, but distant from, the lens axis to be focused in a slightly different place than beams close to the axis. This manifests itself as a blurring of the image. Lenses in which closer-to-ideal, non-spherical surfaces are used are called aspheric lenses. These were formerly complex to make and often extremely expensive, but advances in technology have greatly reduced the manufacturing cost for such lenses. Spherical aberration can be minimised by careful choice of the curvature of the surfaces for a particular application: for instance, a plano-convex lens which is used to focus a collimated beam produces a sharper focal spot when used with the convex side towards the beam source.
Coma[සංස්කරණය]
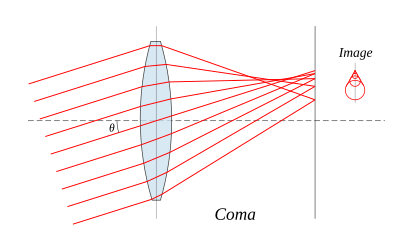
Another type of aberration is coma, which derives its name from the comet-like appearance of the aberrated image. Coma occurs when an object off the optical axis of the lens is imaged, where rays pass through the lens at an angle to the axis θ. Rays which pass through the centre of the lens of focal length f are focused at a point with distance f tan θ from the axis. Rays passing through the outer margins of the lens are focused at different points, either further from the axis (positive coma) or closer to the axis (negative coma). In general, a bundle of parallel rays passing through the lens at a fixed distance from the centre of the lens are focused to a ring-shaped image in the focal plane, known as a comatic circle. The sum of all these circles results in a V-shaped or comet-like flare. As with spherical aberration, coma can be minimised (and in some cases eliminated) by choosing the curvature of the two lens surfaces to match the application. Lenses in which both spherical aberration and coma are minimised are called bestform lenses.
Chromatic aberration[සංස්කරණය]
Chromatic aberration is caused by the dispersion of the lens material—the variation of its refractive index, n, with the wavelength of light. Since, from the formulae above, f is dependent upon n, it follows that different wavelengths of light will be focused to different positions. Chromatic aberration of a lens is seen as fringes of colour around the image. It can be minimised by using an achromatic doublet (or achromat) in which two materials with differing dispersion are bonded together to form a single lens. This reduces the amount of chromatic aberration over a certain range of wavelengths, though it does not produce perfect correction. The use of achromats was an important step in the development of the optical microscope. An apochromat is a lens or lens system which has even better correction of chromatic aberration, combined with improved correction of spherical aberration. Apochromats are much more expensive than achromats.
Different lens materials may also be used to minimise chromatic aberration, such as specialised coatings or lenses made from the crystal fluorite. This naturally occurring substance has the highest known Abbe number, indicating that the material has low dispersion.
Other types of aberration[සංස්කරණය]
Other kinds of aberration include field curvature, barrel and pincushion distortion, and astigmatism.
Aperture diffraction[සංස්කරණය]
Even if a lens is designed to minimize or eliminate the aberrations described above, the image quality is still limited by the diffraction of light passing through the lens' finite aperture. A diffraction-limited lens is one in which aberrations have been reduced to the point where the image quality is primarily limited by diffraction under the design conditions.
සංයුක්ත කාච[සංස්කරණය]
සරල කාච භාවිත කරන විට ඉහත සාකච්ඡා කළ පරිදි ආලෝකය අප්රේරණයකට ලක්වේ. බොහෝ අවස්ථාවලදී මෙම අප්රේරණයේ අවම කරගැනීම සඳහා එකිනෙකට අනුපූරක අප්රේරණ සහිත සරල කාච සංයුක්තයන් භාවිතා කරයි. සංයුක්ත කාචයක් යනු වෙනස් හැඩ සහිත සරල කාච එකතුවකි. ඒවා වෙනස් වර්තන අංක සහිත ද්රව්යයවලින් සාදා ඇති අතර පොදු අක්ෂයක පිහිටන පරිදි එකක් පිටුපස එකක් වන ලෙස සකසා ඇත.
මේ ආකාරයට කාච සම්බන්ධ භාවිතාවන සරලම අවස්ථාව වනුයේ කාච එකිනෙක ස්පර්ශව තැබීමයි. එසේ තැබූ කාච නාභි දුර f1 හා f2 වන සිහින් කාච වේනම් සංයුක්ත කාචයේ නාභි දුර
- වේ.
කාචයක බලය 1/f වන බැවින් සිහින් කාච ස්පර්ශ කිරීමේදී ඒවායේ බලයන් ආකලනය කළ හැකි බව ඉන් පෙන්ණුම් කරයි.
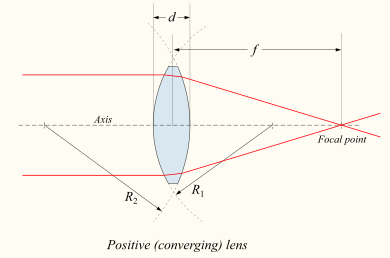
කුඩා තුනී කාච දෙකක් එකිනෙකට කුඩා d දුරකින් ඈත්ව තබා ඇති විට කළ විට , සංයුක්ත කාචයේ නාභියට දුරට දෙවන කාචයේ සිට ඇති දුර BFLපසු නාභි දුර යැයි කියනු ලැබේ. මෙය දෙනු ලබන්නේ,
මෙහි d ශූන්යයට ආසන්න වන විට BFL අගය , ස්පර්ශව තැබූ සිහින් කාචවල සංයුක්ත නාභි දුරට ක්රමයෙන් ආසන්න වේ.
කාච අතර දුර කාච දෙකේ නාභි දුරයන්හි ඓක්යයට සමාන වන විට BFL අගය අනන්ත වේ. මෙය, සමාන්තර ආලෝක කදම්භයක් තවත් සමාන්තර ආලෝක කදම්භයක් බවට පරිණාමනය කරන කාච යුගලයකට අනුරූප වේ. මෙවැනි පද්ධතියක් කදම්භයේ ශුද්ධ අභිසරණයක් හෝ අපසරණයක් සිදු නොකරන බැවින් afocal (නාභීය නොවන) යැයි කියනු ලැබේ. මෙවැනි දුරකින් තැබු කාච දෙකක් මගින් සරලතම වර්ගයේ ප්රකාශ දුරේක්ෂයක් ලබාදේ.
මෙවැනි පද්ධතිය මගින් සමාන්තර කදම්භයක අපසාරීතාව වෙනස් නොකරන නමුත් එය කදම්භයේ පළල වෙනස් කරයි. ඒ අනුව දුරේක්ෂයේ විශාලනය දෙනු ලබන්නේ ,
- මගිනි.
මෙය ප්රධාන කදම්භයේ පළල ප්රතිදාන කදම්භයේ පළලට ඇති අනුපාතයට සමාන වේ.
ලකුණු සම්මුතිය - උත්තල කාච දෙකක් (f1 > 0 , f2 > 0) සහිත දූරේක්ෂයක් මගින් සෘණ විශාලනයක් සහිත එනම්, යටිකුරු ප්රතිබිම්භයක් ලබාදේ. උත්තල කාචයක් හා අවතල කාචයක් (f1 > 0 > f2) සහිත දුරේක්ෂයක් මගින් ධන විශාලනයක් හෙවත් උඩුකුරු ප්රතිබිම්භයක් ලබා දේ.
කාච වල ප්රයෝජන[සංස්කරණය]
මිටකට හෝ ආධාරකයක් සහිතව රාමුවකට සවිකළ තනි උත්තල කාච, විශාලක කාච වේ.
අවිදුර දෘෂ්ටිකත්වය, උපරිදෘෂ්ඨිය, වෘද්ධ දෘෂ්ටිකතාව (හතළිස් ඇඳිරිය) හා විෂම දෘෂ්ටිකතාව වැනි දෘශ්ය ආබාධයන් නිවැරදි කිරීමට කාච භාවිතා වේ. කාච වෙනත් කාර්යයන් සේ නිවැරදිව අක්ෂ සමමිතියට ලබාගැනීමට භාවිතා කරයි. උපනෙත්/කණ්ණාඩි කාච ආසන්න වශයෙන් පමණක් සමමිතිකය. ඒවා සාමාන්යයෙන් දළ වශයෙන් ඕවලාකාර, රවුම් නැති රාමුවකට යෝග්යවන සේ හැඩ ගස්වා ඇත. ප්රකාශ කේන්ද්රය අක්ෂි ගෝලයට ඉහළින් ඉදිරියෙන් ස්ථාන ගත කර ඇත. ඒවායේ වක්රතායට විෂම දෘෂ්ටිකතාවයේ නිවැරදි කිරීම් සදහා අක්ෂය සමමිතිකව නැත. අව් කණ්ණාඩි කාච වර්තනයකින් තොරව ආලෝකය අඩු කිරීමට නිර්මාණය කර ඇත.
තවත් ප්රයෝජනයක් වන්නේ ඒකාෂික, දුර දර්ශකය, දුරේක්ෂ්ය, තිතනේක්ෂය, දුරේක්ෂි අක්ෂි සමමිතිය, තියොඩොලයිට්ටුව, අන්වීක්ෂ්ය, කැමරාව (ඡායාරූපි කාච) හා ප්රතික්ෂේපකය වැනි මුර්තන පද්ධතිවල භාවිතා වේ. මින් සමහර උපකරණ අසත්ය ප්රතිබිම්භයක් මිනිස් ඇස හා යෙදීමේදී නිපදවයි. අනෙක්වා ඡායාරූපි පටකය හෝ ප්රකාශ සංවේදකවල ග්රහණය කරගත හැකි සත්ය ප්රතිබිම්භයක් නිපදවයි.
උත්තල කාච අනන්තයේ ඇති වස්තුවක ප්රතිබිම්භයක් එහි නාභියේ තනයි. හිරු ප්රතිබිම්භයක් එහි නාභියේ තනයි. හිරු ප්රතිබිම්භයක් ගත කළහොත් කාචය මත පතනය වන සියළුම අධෝරක්ත ශක්තිය කුඩා ප්රතිබිම්භය මතට එක් තැන් වේ.විශාල කාච දහන ලක්ෂයට ප්රතිබිම්භය පතිත වන සේ දහනය වන සුළු වස්තුවක් රත් කිරීමට තරම් වූ ශක්තියක් යොමු කරයි. වසර සිය ගණනක් පුරා ආසන්න වශයෙන් ප්රකාශීය ලෙස නිවැරදි වීම පවා අවශ්ය නොවූ කාච දාහක කාච ලෙස භාවිතා කර ඇත. නූතන යෙදීම් වන්නේ විශාල මිල අධික කෝෂ භාවිතා නොකරමින් සාපේක්ෂව විශාල කාච භාවිතයෙන් සාපේක්ෂව කුඩා ප්රකාශ වෝල්ටීය කෝෂ වෙත සුර්ය්ය ශක්තිය යොමු කරමින් වැඩි ශක්තියක් නෙලා ගැනීමයි.
රේඩියෝ තාරකා විද්යාව හා රේඩාර් පද්ධති බොහෝ විට පාර විද්යුත් කාච භාවිතා කරයි. බහුලව එකතු කිරීමේ ඇන්ටනාවකට විද්යුත් චුම්භක විකිරණ වර්තනය කරන කාච ඇන්ටනා වේ. 2020 දී පර්යේෂණයට එකතු වීමට නියමිත ඝන කිලෝමීටර පෙළ රේඩියෝ දුරේක්ෂය පෙර ඇන්ටනා වලට වඩා තිස් ගුණයක් විශාල එකතු කිරීමේ ප්රදේශයක් ගත හැකි කාච වැඩට යොදා ගනු ඇත.
ආශ්රිත ලිපි[සංස්කරණය]
- කැමරා කාච
- Anti-fogging treatment of optical surfaces
- Axicon
- Back focal plane
- Bokeh
- Cardinal point (optics)
- Corrective lens
- Cylindrical lens
- Eyepiece
- F-number
- Fresnel lens
- Gradient index lens
- Gravitational lens
- History of lensmaking
- Lens (anatomy)
- List of lens designs
- Microscope
- Microlens
- Numerical aperture
- Optical coatings
- Optical lens design
- Optical lenticular
- Photochromic lens
- Photographic lens
- Prime lens
- Prism (optics)
- Ray tracing
- Sunglass lens
- Superlens
- Telescope
- Zoom lens
මූලාශ්ර[සංස්කරණය]
Bibliography[සංස්කරණය]
- Hecht, Eugene (1987). Optics (2nd ed.). Addison Wesley. ISBN 0-201-11609-X. Chapters 5 & 6.
- Hecht, Eugene (2002). Optics (4th ed.). Addison Wesley. ISBN 0-321-18878-0.
- Greivenkamp, John E. (2004). Field Guide to Geometrical Optics. SPIE Field Guides vol. FG01. SPIE. ISBN 0-8194-5294-7.
බාහිර සබැඳුම්[සංස්කරණය]

- Applied photographic optics Book
- Book- The properties of optical glass
- Handbook of Ceramics, Glasses, and Diamonds
- Optical glass construction
- History of Optics (audio mp3) by Simon Schaffer, Professor in History and Philosophy of Science at the University of Cambridge, Jim Bennett, Director of the Museum of the History of Science at the University of Oxford and Emily Winterburn, Curator of Astronomy at the National Maritime Museum (recorded by the BBC).
- a chapter from an online textbook on refraction and lenses සංරක්ෂණය කළ පිටපත 2009-12-17 at the Wayback Machine
- Thin Spherical Lenses on Project PHYSNET.
- Lens article at digitalartform.com සංරක්ෂණය කළ පිටපත 2016-03-04 at the Wayback Machine
- Article on Ancient Egyptian lenses
- picture of the Ninive rock crystal lens සංරක්ෂණය කළ පිටපත 2007-05-16 at the Wayback Machine
- Do Sensors “Outresolve” Lenses? සංරක්ෂණය කළ පිටපත 2008-07-01 at the Wayback Machine; on lens and sensor resolution interaction.
- Fundamental optics
Simulations[සංස්කරණය]
- Learning by Simulations - Concave and Convex Lenses
- OpticalRayTracer - Open source lens simulator (downloadable java)
[[gan:透鏡]
- Numbered list item

![{\displaystyle {\frac {1}{f}}=(n-1)\left[{\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}+{\frac {(n-1)t}{nR_{1}R_{2}}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/635ac2f8be11553b913727b8ea880bc509893ddb)





![{\displaystyle {\frac {1}{f}}\approx \left(n-1\right)\left[{\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c633e7b574392e54107881cd2e697e0ba9a68877)